题目内容
3.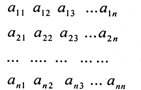 如图表:现有n2(n≥4)个正数排列成n行n列方阵,符号aij(1≤i≤n,1≤j≤n,i,j∈N*)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都相等.若a11=2,a24=a32=16,则aij=2i•j.
如图表:现有n2(n≥4)个正数排列成n行n列方阵,符号aij(1≤i≤n,1≤j≤n,i,j∈N*)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都相等.若a11=2,a24=a32=16,则aij=2i•j.
分析 设第一行的公差为d,等比数列的公比为q,进而根据若a11=2,a24=a32=16,利用等差数列和等比数列的通项公式可得方程组求得q和d,进而求得aij.
解答 解:设第一行的公差为d,等比数列的公比为q,
依题意可知(2+3d)q=(2+d)q2=16,
解得q=2,d=2,
∴aij=[2+2(j-1)]2i-1=j•2i,
故答案为:j•2i.
点评 本题主要考查了等差数列和等比数列的通项公式.本题主要考查了学生对等差数列和等比数列的理解和灵活运用.

练习册系列答案
相关题目
11.函数f(x)=$\frac{1}{3}$x3+x在点处(1,$\frac{4}{3}$)的切线与坐标轴围成的三角形的面积为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{1}{9}$ |
15.某班主任对全班50名学生进行了作业量多少的调查,得到如下列联表:
经计算得K2≈5.059,则有97.5%的把握认为喜欢玩电脑游戏与认为作业多有关系.
| 认为作业多 | 认为作业不多 | 合计 | |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 合计 | 26 | 24 | 50 |