题目内容
已知M={y|y=x2+1}，N={x|x2+y2=2}，则M∩N=________．
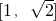
分析：先化简两个集合，再利用两个集合的交集的定义求出M∩N．
解答：因为：M={y|y=x2+1}，N={x|x2+y2=2}，
故：M={y|y≥1}，N={x|-
≤x≤}．∴M∩N=[1，
]故答案为：[1，
]．点评：本题考查两个集合的交集的定义以及求函数的值域的方法，确定两个集合中元素的取值范围是解题的关键和难点．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
（x∈R，a∈R，a是常数），且
（其中O为坐标原点）．
时，f（x）的最大值为4，求a的值．