题目内容
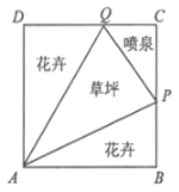
【题目】如图所示，我市某居民小区拟在边长为1百米的正方形地块
上划出一个三角形地块
种植草坪，两个三角形地块
与
种植花卉，一个三角形地块
设计成水景喷泉，四周铺设小路供居民平时休闲散步，点
在边
上，点
在边
上，记
．
（1）当
时，求花卉种植面积
关于
的函数表达式，并求的最小值；
（2）考虑到小区道路的整体规划，要求
，请探究
是否为定值，若是，求出此定值，若不是，请说明理由．
【答案】（1）
，
]；最小值为
（2）
是定值，且
．
【解析】
（1）根据三角函数定义及，表示出
，进而求得
.即可用
表示出
，
（2）设
，利用正切的和角公式求得
，由
求得
的等量关系.进而求得的值，即可求得的值.
（1）∵边长为1百米的正方形
中，
，，
∴
，
，
∴
，其中
∴当
时，
即
时，S取得最小值为
．
（2）设，
则
，
在
中，
，在
中，
，
∴
，
∵，
∴
，整理可得
，
∴
，
∴
，
∴是定值，且．
练习册系列答案
相关题目
【题目】某市推行“共享汽车”服务，租用汽车按行驶里程加用车时间收费，标准是“1元/公里+0.2元/分钟”，刚在该市参加工作的小刘拟租用“共享汽车“上下班.单位同事老李告诉他：“上下班往返总路程虽然只有10公里，但偶尔上下班总共也需要用时大约1小时”，并将自己近50天往返开车的花费时间情况统计如下
时间（分钟） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） |
次数ξ | 8 | 18 | 14 | 8 | 2 |
将老李统计的各时间段频率视为相应概率，假定往返的路况不变，而且每次路上开车花费时间视为用车时间.
（1）试估计小刘每天平均支付的租车费用（每个时间段以中点时间计算）；
（2）小刘认为只要上下班开车总用时不超过45分钟，租用“共享汽车”为他该日的“最优选择”，小刘拟租用该车上下班2天，设其中有ξ天为“最优选择”，求ξ的分布列和数学期望.
