题目内容
我们知道，如果定义在某区间上的函数
满足对该区间上的任意两个数
、
，
总有不等式
成立，则称函数为该区间上的向上凸函数（简称上凸）.
类比上述定义，对于数列
，如果对任意正整数
，总有不等式：
成立，
则称数列为向上凸数列（简称上凸数列）. 现有数列满足如下两个条件：
（1）数列为上凸数列，且
；
（2）对正整数（
），都有
，其中
.
则数列中的第五项
的取值范围为 ★ .
.
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案
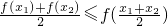成立，则称函数f（x）为该区间上的向上凸函数（简称上凸）．类比上述定义，对于数列{an}，如果对任意正整数n，总有不等式：
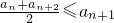成立，则称数列{an}为向上凸数列（简称上凸数列）．现有数列{an}满足如下两个条件：
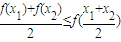成立，则称函数f（x）为该区间上的向上凸函数（简称上凸）．类比上述定义，对于数列{an}，如果对任意正整数n，总有不等式：
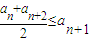成立，则称数列{an}为向上凸数列（简称上凸数列）．现有数列{an}满足如下两个条件：
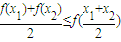成立，则称函数f（x）为该区间上的向上凸函数（简称上凸）．类比上述定义，对于数列{an}，如果对任意正整数n，总有不等式：
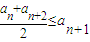成立，则称数列{an}为向上凸数列（简称上凸数列）．现有数列{an}满足如下两个条件：
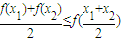成立，则称函数f（x）为该区间上的向上凸函数（简称上凸）．类比上述定义，对于数列{an}，如果对任意正整数n，总有不等式：
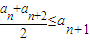成立，则称数列{an}为向上凸数列（简称上凸数列）．现有数列{an}满足如下两个条件：