题目内容
设
，
，且
、
夹角为
，则
等于（ ）
A． | B． | C． | D． |
A
解析试题分析：因为，，且、夹角为，所以
，所以
所以
考点：本小题主要考查向量的数量积的计算和向量的模的求解，考查学生的运算求解能力.
点评：求向量的模，要先求向量的模的平方.
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图
为互相垂直的单位向量，向量
可表示为
A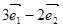． | B． |
C． | D． |
与向量
=（
，1），
=（1，
）的夹角相等且模为
的向量为 （ ）
A． |
B． |
C． |
D． |
如图所示，点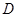
是△
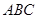的边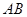
上的中点，则向量
( )
A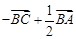． | B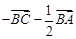． | C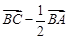． | D． |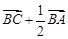
在空间四边形
中，
，
，
，
，
分别为
、
的中点，则
可表示为（ ）
A． | B． |
C． | D． |
向量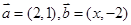
，若
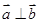，则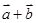
= （ ）
| A．（3，-1） | B．（-3，1） | C．（-2，-1） | D．（2 ，1） |
，
为互相垂直的单位向量，向量
，
，且
与
的夹角为锐角，则实数
的取值范围是（ ）
已知两点
为坐标原点，点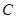
在第二象限，且
，设
则
等于 （ ）
A． | B．2 | C． | D．1 |
已知向量
，则向量
的夹角为 ( )
A． | B． | C． | D． |