题目内容
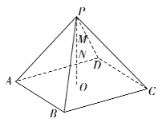
【题目】如图，在四棱锥
中，顶点P在底面的投影
恰为正方形ABCD的中心且
，设点M，N分别为线段PD，PO上的动点，已知当
取得最小值时，动点M恰为PD的中点，则该四棱锥的外接球的表面积为____________．
A.
B.
C.
D.
【答案】A
【解析】
根据已知条件可知四棱锥为正四棱锥；在
上取一点
，使得
，从而可知
三点共线时，
取最小时，且最小值为
；由三线合一性质可确定
；求得
后，利用勾股定理构造关于外接球半径的方程，解方程求得外接球半径
，代入球的表面积公式可求得结果.
四边形
为正方形，顶点
在底面投影
为正方形中心
四棱锥
为正四棱锥
在上取一点，使得，则
三点共面 
三点共线时，最小，最小值为
取最小值时，
为
中点 
为中点
又当
时，最小 
设四棱锥外接球半径为
则
，解得：
四棱锥外接球的表面积：
本题正确选项：
练习册系列答案
阅读快车系列答案
相关题目
