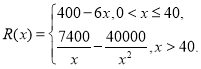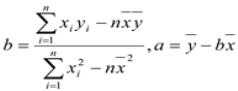题目内容
【题目】已知:以点![]() (
(![]() )为圆心的圆与
)为圆心的圆与![]() 轴交
轴交
于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线![]() 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程.
【答案】(1)根据条件写成圆的方程,求出点A,B的坐标,进而写出△OAB的面积即可得证;
(2)![]()
【解析】试题分析:(1)设出圆C的方程,求得A、B的坐标,再根据S△AOB=![]() OAOB,计算可得结论.
OAOB,计算可得结论.
(2)设MN的中点为H,则CH⊥MN,根据C、H、O三点共线,KMN=﹣2,由直线OC的斜率![]() ,求得t的值,可得所求的圆C的方程.
,求得t的值,可得所求的圆C的方程.
试题解析:
(1)![]() ,
,![]() .
.
设圆![]() 的方程是
的方程是 ![]()
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]()
![]() ,即:
,即:![]() 的面积为定值.
的面积为定值.
(2)![]()
![]() 垂直平分线段
垂直平分线段![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程是
的方程是![]() .
.
![]() ,解得:
,解得:![]()
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() ,圆
,圆![]() 与直线
与直线![]() 相交于两点.
相交于两点.
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() 圆
圆![]() 与直线
与直线![]() 不相交,
不相交,![]() 不符合题意舍去.
不符合题意舍去.
![]() 圆
圆![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目
【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(1)试估计该年级成绩![]() 分的学生人数;
分的学生人数;
(2)已知样本中成绩在![]() 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.