题目内容
已知点A、B、C依次为直线l上三个定点,动点P(P∈l)恒满足∠APB=∠BPC,点P与直线l在确定的平面内,求动点P的轨迹方程,并说明轨迹是什么曲线.
解:以点B为原点,l为x轴建立直角坐标系(如下图),设A(-a,0)、C(c,0)(a>0,c>0),P点坐标为(x,y).
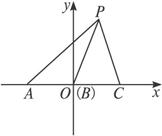
由∠APB=∠BPC≠0,得
![]() =
=![]() =
=![]() .
.
∴![]() =
=![]() .
.
化简,得(a2-c2)x2+(a2-c2)y2-2ac(a+c)x=0.
(1)当a=c时,P点轨迹为y轴(除去原点);
(2)当a≠c时,方程化为x2+y2-![]() x=0,轨迹是以(
x=0,轨迹是以(![]() ,0)为圆心、
,0)为圆心、![]() 为半径的圆,但不包括点(0,0)和(
为半径的圆,但不包括点(0,0)和(![]() ,0).
,0).

练习册系列答案
相关题目

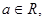 函数
函数 。
。 在区间
在区间 上最小值
上最小值 ;
; 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围;
的取值范围; ,B
,B ,C
,C ,从左到右依次是函数
,从左到右依次是函数 图象上三点,且这三点不共线,求证:
图象上三点,且这三点不共线,求证: 是钝角三角形。
是钝角三角形。