题目内容
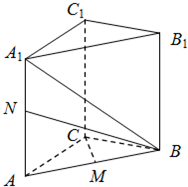 (2012•北京模拟)如图,三棱柱ABC-A1B1C1的侧棱A1A垂直于底面ABC,A1A=2,AC=CB=1,∠BCA=90°,M、N分别是AB、A1A的中点.
(2012•北京模拟)如图,三棱柱ABC-A1B1C1的侧棱A1A垂直于底面ABC,A1A=2,AC=CB=1,∠BCA=90°,M、N分别是AB、A1A的中点.(1)求BN的长;
(2)求证:A1B⊥CM.
分析:(1)利用勾股定理结合AC=CB=1,∠BCA=90°,可求出AB的长,由A1A=2,N是A1A的中点,可求出AN的长,解直角三角形NAB可得BN的长;
(2)由等腰三角形“三线合一”可得CM⊥AB.由已知中A1A⊥底面ABC,结合线面垂直的定义可得A1A⊥CM,进而利用线面垂直的判定定理可得CM⊥平面ABB1A1,最后由线面垂直的定义可得A1B⊥CM.
(2)由等腰三角形“三线合一”可得CM⊥AB.由已知中A1A⊥底面ABC,结合线面垂直的定义可得A1A⊥CM,进而利用线面垂直的判定定理可得CM⊥平面ABB1A1,最后由线面垂直的定义可得A1B⊥CM.
解答:解:(1)因为∠BCA=90°,AC=CB=1,
所以AB=
.
因为A1A⊥底面ABC,且AB?底面ABC,
所以A1A⊥AB.
又A1A=2,N是A1A的中点,
所以NA=1.
所以BN=
=
.
证明:(2)在△ABC中,因为AC=CB,M是AB的中点,
所以CM⊥AB.
又A1A⊥底面ABC,且CM?底面ABC,
所以A1A⊥CM.
因为A1A∩AB=A,
所以CM⊥平面ABB1A1.
又A1B?平面ABB1A1,
所以A1B⊥CM.
所以AB=
| 2 |
因为A1A⊥底面ABC,且AB?底面ABC,
所以A1A⊥AB.
又A1A=2,N是A1A的中点,
所以NA=1.
所以BN=
| 1+2 |
| 3 |
证明:(2)在△ABC中,因为AC=CB,M是AB的中点,
所以CM⊥AB.
又A1A⊥底面ABC,且CM?底面ABC,
所以A1A⊥CM.
因为A1A∩AB=A,
所以CM⊥平面ABB1A1.
又A1B?平面ABB1A1,
所以A1B⊥CM.
点评:本题考查的知识点是直线与平面垂直的性质定理,直线与平面垂直的判定定理,空间图形的位置关系的简单命题,难度中档

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 (2012•北京模拟)如图,在四棱锥P-ABCD中,PA⊥平面AC,且四边形ABCD是矩形,则该四棱锥的四个侧面中是直角三角形的有( )
(2012•北京模拟)如图,在四棱锥P-ABCD中,PA⊥平面AC,且四边形ABCD是矩形,则该四棱锥的四个侧面中是直角三角形的有( ) (2012•北京模拟)甲、乙、丙、丁四个人进行传球练习,每次球从一个人的手中传入其余三个人中的任意一个人的手中.如果由甲开始作第1次传球,经过n次传球后,球仍在甲手中的所有不同的传球种数共有an种.
(2012•北京模拟)甲、乙、丙、丁四个人进行传球练习,每次球从一个人的手中传入其余三个人中的任意一个人的手中.如果由甲开始作第1次传球,经过n次传球后,球仍在甲手中的所有不同的传球种数共有an种.