Question

（2012•北京模拟）甲、乙、丙、丁四个人进行传球练习，每次球从一个人的手中传入其余三个人中的任意一个人的手中．如果由甲开始作第1次传球，经过n次传球后，球仍在甲手中的所有不同的传球种数共有a_n种．
（如，第一次传球模型分析得a₁=0．）
（1）求 a₂，a₃的值；
（2）写出 a_n+1与 a_n的关系式（不必证明），并求 a_n=f（n）的解析式；
（3）求 

an

an+1

的最大值．

Answer 1

分析：（1）通过画图，作出符合题意的示意图，加以总结即可得到 a₂，a₃的值；
（2）计算前几项，可发现规律：a_n+1+an=3n（n=1，2，3，…）．利用待定系数法，得到数列 {an-

1

4

×3n}是首项为-

3

4

，公比为-1的等比数列．最后借助于等比数列的通项公式，即可算出 a_n=f（n）的解析式；
（3）分n为偶数和n为奇数两种情况，讨论

an

an+1

的单调性并结合不等式的性质进行推理，即可得到当n=2时，

a2

a3

=

1

2

为 

an

an+1

的最大值．

解答：解：（1）可画出示意图：

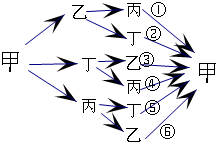
可得经过两次传球回到甲手中的所有不同种数为3；经过3次传球回到甲手中的所有不同种数为6．
因此可得：得 a₂=3，a₃=6．
（2）依题意有  a₁=0，且 a_n+1+an=3n（n=1，2，3，…）．
将 a_n+1+an=3n变形为 an+1-

1

4

×3n+1=-(an-

1

4

×3n)，
从而数列 {an-

1

4

×3n}是首项为a1-

3

4

=-

3

4

，公比为-1的等比数列．
∴an-

1

4

×3n=-

3

4

×(-1)n-1，可得 an=

3n

4

+(-1)n•

3

4

（n=1，2，3，…）．
（3）①当n是偶数时，

an

an+1

  =  

3n 4 + 3 4

3n+1 4 - 3 4

  =  

3n+3

3n+1-3

  =  

1

3

+

4

3n+1-3

，为关于n的单调递减函数
∴当n是偶数时，

an

an+1

随n的增大而减小，从而，当n是偶数时，

an

an+1

的最大值是 

a2

a3

=

1

2

．
②当n是奇数时，

an

an+1

  =  

3n 4 - 3 4

3n+1 4 + 3 4

  =  

3n-3

3n+1+3

  =  

1

3

-

4

3n+1+3

，为关于n的单调增减函数
∴当n是奇数时，

an

an+1

随n的增大而增大，且 

an

an+1

=

1

3

-

4

3n+1+3

＜

1

3

＜

1

2

．
综上，

an

an+1

的最大值是 

1

2

．

点评：本题考查了函数的单调性、指数函数的单调性、函数模型（指数函数）的应用、等比数列的概念、等比数列的通项公式，以及用等比数列知识解决相应的问题等知识点，属于中档题．