题目内容
已知不等式ax2-4ax+3a+6≥0对一切实数x恒成立，求关于x的方程
=|a-4|+2的根的取值范围.
思路分析:首先根据条件求出a的取值范围，然后对=|a-4|+2进行变形得x=(|a-4|+2)·(a+1),再由a的范围求x的范围.
解:由已知可得a=0或
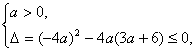
∴0≤a≤6.
方程
=|a-4|+2的根是x=(|a-4|+2)(a+1).
①当0≤a＜4时，x=(6-a)(a+1)=-(a-
)2+
∈［6,
］.
②当4≤a≤6时，x=(a-2)(a+1)=(a-
)2-
∈［10,28］.
综合①②可得x的取值范围为［6,28］.
练习册系列答案
相关题目
已知不等式ax2+bx+c＞0的解集为{x|2＜x＜4}，则不等式cx2+bx+a＜0的解集为（ ）
A、{x|x＞
| ||||
B、{x|x＜
| ||||
C、{x|
| ||||
D、{x|x＞
|