题目内容
设不等式2(log x)2+9(log
x)2+9(log x)+9≤0的解集为M,求当x∈M时,函数f(x)=(log2
x)+9≤0的解集为M,求当x∈M时,函数f(x)=(log2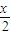 )•(log2
)•(log2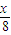 )的最大值和最小值.
)的最大值和最小值.
【答案】分析:由2(log x)2+9(log
x)2+9(log x)+9≤0可知-3≤log
x)+9≤0可知-3≤log x≤-
x≤- ,从而推导出
,从而推导出 ≤log2x≤3,再由f(x)=(log2x-1)(log2x-3(log2x-2)2-1能够推导出函数f(x)=(log2
≤log2x≤3,再由f(x)=(log2x-1)(log2x-3(log2x-2)2-1能够推导出函数f(x)=(log2 )(log2
)(log2 )的最大值和最小值.
)的最大值和最小值.
解答:解:∵2(log x)2+9(log
x)2+9(log x)+9≤0,
x)+9≤0,
∴(2log x+3)(log
x+3)(log x+3)≤0.
x+3)≤0.
∴-3≤log x≤-
x≤- .
.
即log (
( )-3≤log
)-3≤log x≤log
x≤log (
( )-
)-
∴( )-
)- ≤x≤(
≤x≤( )-3,即2
)-3,即2 ≤x≤8.
≤x≤8.
从而M=[2 ,8].
,8].
又f(x)=(log2x-1)(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1.
∵2 ≤x≤8,
≤x≤8,
∴ ≤log2x≤3.
≤log2x≤3.
∴当log2x=2,即x=4时ymin=-1;
当log2x=3,即x=8时,ymax=0.
点评:先解不等式求出解集为M,再利用对数函数的性质和二次函数的最值求函数f(x)=(log2 )•(log2
)•(log2 )的最大值和最小值.
)的最大值和最小值.
 x)2+9(log
x)2+9(log x)+9≤0可知-3≤log
x)+9≤0可知-3≤log x≤-
x≤- ,从而推导出
,从而推导出 ≤log2x≤3,再由f(x)=(log2x-1)(log2x-3(log2x-2)2-1能够推导出函数f(x)=(log2
≤log2x≤3,再由f(x)=(log2x-1)(log2x-3(log2x-2)2-1能够推导出函数f(x)=(log2 )(log2
)(log2 )的最大值和最小值.
)的最大值和最小值.解答:解:∵2(log
 x)2+9(log
x)2+9(log x)+9≤0,
x)+9≤0,∴(2log
 x+3)(log
x+3)(log x+3)≤0.
x+3)≤0.∴-3≤log
 x≤-
x≤- .
.即log
 (
( )-3≤log
)-3≤log x≤log
x≤log (
( )-
)-
∴(
 )-
)- ≤x≤(
≤x≤( )-3,即2
)-3,即2 ≤x≤8.
≤x≤8.从而M=[2
 ,8].
,8].又f(x)=(log2x-1)(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1.
∵2
 ≤x≤8,
≤x≤8,∴
 ≤log2x≤3.
≤log2x≤3.∴当log2x=2,即x=4时ymin=-1;
当log2x=3,即x=8时,ymax=0.
点评:先解不等式求出解集为M,再利用对数函数的性质和二次函数的最值求函数f(x)=(log2
 )•(log2
)•(log2 )的最大值和最小值.
)的最大值和最小值. 
练习册系列答案
相关题目
 x)2+9(log
x)2+9(log )•(log2
)•(log2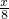 )的最大值和最小值.
)的最大值和最小值. x)2+9(log
x)2+9(log x)+9≤0的解集为M,求当x∈M时,函数f(x)=(log2
x)+9≤0的解集为M,求当x∈M时,函数f(x)=(log2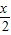 )•(log2
)•(log2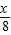 )的最大值和最小值.
)的最大值和最小值. x)2+9(log
x)2+9(log x)+9≤0的解集为M,求当x∈M时,函数f(x)=(log2
x)+9≤0的解集为M,求当x∈M时,函数f(x)=(log2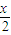 )•(log2
)•(log2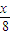 )的最大值和最小值.
)的最大值和最小值.