题目内容
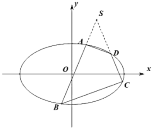
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 分别是椭圆
分别是椭圆![]() :
:![]() (
(![]() )的左右焦点,点
)的左右焦点,点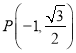 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .若椭圆
.若椭圆![]() 的内接四边形
的内接四边形![]() 的边
的边![]() 的延长线交于椭圆外一点
的延长线交于椭圆外一点![]() ,且点
,且点![]() 的横坐标为1,记直线
的横坐标为1,记直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)求椭圆定义可知![]() ,点
,点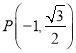 代入即可得出结果;
代入即可得出结果;
(2)设![]() ,
,![]() ,因为
,因为![]() 的延长线交于椭圆外一点
的延长线交于椭圆外一点![]() ,且点
,且点![]() 的横坐标为1,于是有
的横坐标为1,于是有![]() ,将直线与椭圆方程联立,结合韦达定理及弦长公式可求得
,将直线与椭圆方程联立,结合韦达定理及弦长公式可求得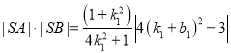 ,
,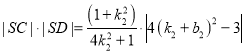 ,根据已知条件
,根据已知条件![]() 化简即可得出结果.
化简即可得出结果.
(1)![]()
![]() ,∴
,∴![]()
点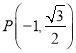 是椭圆
是椭圆![]() 上一点,代入方程:
上一点,代入方程:![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的标准方程:
的标准方程:![]()
(2)设![]() ,
,![]()
![]() 的延长线交于椭圆外一点
的延长线交于椭圆外一点![]() ,且点
,且点![]() 的横坐标为1,于是有
的横坐标为1,于是有![]() ①
①
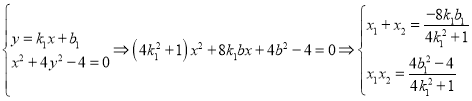 ②
②
于是:![]()
代入②可得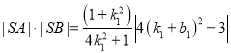
同理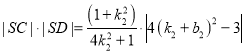
又![]() ,
,![]() 可得:
可得:![]()
∴![]()
法二:(1)由![]() 为椭圆
为椭圆![]() 的左右焦点,
的左右焦点,![]() 为
为![]() 上一点,
上一点,![]()
∴![]() ,∴
,∴![]() ,∴椭圆
,∴椭圆![]()
将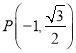 代入可得
代入可得![]()
∴椭圆![]() 的标准方程为
的标准方程为![]()
(2)设![]() ,由
,由![]() 斜率分别为
斜率分别为![]()
则直线![]() 的方程分别为
的方程分别为![]()
将![]() 与
与![]() 联立,设
联立,设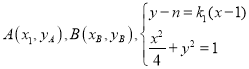
![]()
由韦达定理,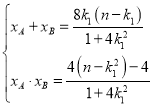
∴![]()
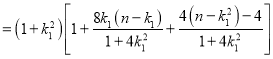
![]()
![]()
同理可证![]()
则由![]() ,得
,得![]()
从而![]()
即![]()
∴![]() ,∴
,∴![]()
又![]() 为
为![]() 的内接四边形,∴
的内接四边形,∴![]() ,∴
,∴![]()

练习册系列答案
相关题目