题目内容
某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系)．根据图象提供的信息解答下列问题：
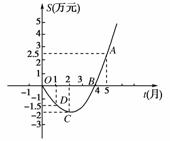
(1)由已知图象上的三点坐标，求累积利润S(万元)与时间t(月)之间的函数关系式；
(2)求截止到第几月末公司累积利润可达到30万元；
(3)求第八个月公司所获利润是多少万元．
解析： (1)由二次函数图象可知，设S与t的函数关系式为
S＝at2＋bt＋c.
无论哪个均可解得a＝
，b＝－2，c＝0，
∴所求函数关系式为S＝t2－2t.
(2)把S＝30代入，得30＝t2－2t，
解得t1＝10，t2＝－6(舍去)，
∴截止到第10个月末公司累积利润可达到30万元．
(3)把t＝7代入，得S＝×72－2×7＝
＝10.5(万元)，
把t＝8代入，得
S＝×82－2×8＝16(万元)，
则第八个月获得的利润为
16－10.5＝5.5(万元)，
∴第八个月公司所获利润为5.5万元．
小学夺冠AB卷系列答案
.有一组实验数据如下表所示：
| t | 1 | 2 | 3 | 4 | 5 |
| s | 1.5 | 5.9 | 13.4 | 24.1 | 37 |
下列所给函数模型较适合的是( )
A．y＝logax(a>1) B．y＝ax＋b(a>1)
C．y＝ax2＋b(a>0) D．y＝logax＋b(a>1)
已知函数f(x)的图象是连续不断的，有如下的x，f(x)对应值表：
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(x) | 123.5 | 21.5 | －7.82 | 11.57 | －53.7 | －126.7 | －129.6 |
那么函数f(x)在区间[1,6]上的零点至少有( )
A．2个 B．3个
C．4个 D．5个
则f(f(2))＝( )