题目内容
在我校“学雷锋”活动月的一次活动中,甲、乙、丙、丁戊五位同学随机地选择承担A、B、C、D四项不同任务中的一项.
(1)若每项任务至少有一个同学承担,求甲、乙两人不同时承担同一项任务的概率;
(2)设这五位同学选择承担任务的项数为随机变量ξ,求ξ的分布列及数学期望Eξ.
解:(1)设甲、乙两人同时承担同一项任务为事件A,则P(A)= =
=
∴甲、乙两人不同时承担同一项任务的概率为P( )=1-P(A)=
)=1-P(A)=
(2)随机变量ξ的可能取值为1,2,3,4,则
P(ξ=1)= =
=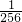 ;P(ξ=2)=
;P(ξ=2)= =
= ;P(ξ=3)=
;P(ξ=3)= ;P(ξ=4)=
;P(ξ=4)= =
=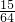 ;
;
∴ξ的分布列为
∴Eξ=1×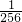 +2×
+2× +3×
+3× +4×
+4×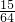 =
= .
.
分析:(1)先求甲、乙两人同时承担同一项任务的概率,再利用对立事件求甲、乙两人不同时承担同一项任务的概率;
(2)确定随机变量ξ的可能取值,求出相应的概率,即可得到ξ的分布列与数学期望.
点评:本题考查概率的计算,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出相应的概率是关键.
 =
=
∴甲、乙两人不同时承担同一项任务的概率为P(
 )=1-P(A)=
)=1-P(A)=
(2)随机变量ξ的可能取值为1,2,3,4,则
P(ξ=1)=
 =
=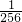 ;P(ξ=2)=
;P(ξ=2)= =
= ;P(ξ=3)=
;P(ξ=3)= ;P(ξ=4)=
;P(ξ=4)= =
=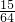 ;
;∴ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P | 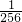 |  |  | 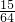 |
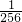 +2×
+2× +3×
+3× +4×
+4×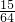 =
= .
.分析:(1)先求甲、乙两人同时承担同一项任务的概率,再利用对立事件求甲、乙两人不同时承担同一项任务的概率;
(2)确定随机变量ξ的可能取值,求出相应的概率,即可得到ξ的分布列与数学期望.
点评:本题考查概率的计算,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出相应的概率是关键.

练习册系列答案
相关题目