题目内容
已知-(1)求sinx-cosx的值;
(2)求 .
.
解:解法1:(1)由sinx+cosx=![]() ,平方得sin2x+2sinxcosx+cos2x=
,平方得sin2x+2sinxcosx+cos2x=![]() .
.
即2sinxcosx=-![]() .
.
∵(sinx-cosx)2=1-2sinxcosx=![]() .
.
又∵-![]() <x<0,∴sinx<0,cosx>0,sinx-cosx<0,
<x<0,∴sinx<0,cosx>0,sinx-cosx<0,
故sinx-cosx=-![]() .
.
(2)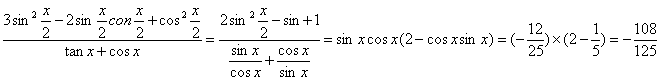 解法2:(1)联立方程
解法2:(1)联立方程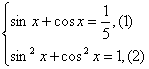
由(1)得sinx=-![]() cosx,将其代入(2),整理得25cos2x-5cosx-12=0,
cosx,将其代入(2),整理得25cos2x-5cosx-12=0,
∴cosx=-![]() 或cosx=
或cosx=![]() .
.
∵-![]() <x<0,∴
<x<0,∴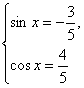
故sinx-cosx=-![]() .
.
(2) 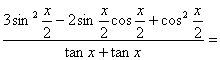
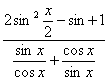 =sinxcosx×(2-cosx-sinx)
=sinxcosx×(2-cosx-sinx)
=![]() ).
).

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
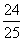 的值.
的值.