题目内容
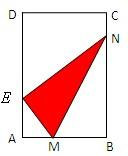 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,MN=l.
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,MN=l.(1)试将l表示成θ的函数;
(2)求l的最小值.
分析:(1)将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,则△MNE≌△MNB,EM+BM,由∠MNB=θ,MN=l.由AB=6cm,我们可得EM+AM=6,然后将EM与BM分别用含θ的式子表示,代入即可得到l表示成θ的函数的解析式.
(2)根据(1)的结论,分析θ角的取值范围,利用导数法求出函数的单调性,进而求出l的最小值.
(2)根据(1)的结论,分析θ角的取值范围,利用导数法求出函数的单调性,进而求出l的最小值.
解答:解:(Ⅰ)由题设,如图所示,△NBM≌△NEM,∠MNB=θ,MN=l,
∴∠AEM=90°-2θ,则MB=lsinθ,AM=l•sinθsin(90°-2θ),
由题设得:AM+MB=lsinθ+l•sinθsin(90°-2θ)=6,
从而得l=
,
即:l=
,l=
由
得:
≤θ≤
,
故:l表示成θ的函数为:l=
,(
≤θ≤
).
(Ⅱ)设:sinθ=t则u=t(1-t2)=t-t3,即u=t-t3,
≤θ≤
,u′=1-3t2令u′=0,得t=
当t<
时,
u′>0,当t>
时,u′<0,所以当t=
时,
u取到最大值:
-
=
,
∴l的最小值为
=
.
∴∠AEM=90°-2θ,则MB=lsinθ,AM=l•sinθsin(90°-2θ),
由题设得:AM+MB=lsinθ+l•sinθsin(90°-2θ)=6,
从而得l=
| 6 |
| sinθ+sinθsin(90°-2θ) |
即:l=
| 6 |
| sinθ+sinθcos2θ |
| 3 |
| sinθ•cos2θ |
由
|
| π |
| 12 |
| π |
| 4 |
故:l表示成θ的函数为:l=
| 3 |
| sinθ•cos2θ |
| π |
| 12 |
| π |
| 4 |
(Ⅱ)设:sinθ=t则u=t(1-t2)=t-t3,即u=t-t3,
| π |
| 12 |
| π |
| 4 |
| ||
| 3 |
| ||
| 3 |
u′>0,当t>
| ||
| 3 |
| ||
| 3 |
u取到最大值:
| ||
| 3 |
| 1 |
| 3 |
| ||
| 3 |
2
| ||
| 9 |
∴l的最小值为
| 3 | ||||
|
9
| ||
| 2 |
点评:在求实际问题对应的函数的解析式,我们一定要进一步分析自变量的取值范围,这不仅是为了让函数的解析式更准确,而且为利用函数的解析式求函数的值域,最值、单调性、奇偶性等打好基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
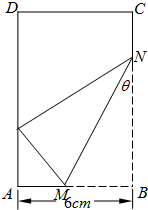 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l.
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l. 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的左边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,则θ的取值范围为
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的左边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,则θ的取值范围为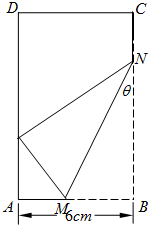 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l.
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l.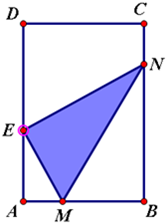 已知矩形纸片ABCD中,AB=6,AD=12,将举行制品的右下角沿线段MN折叠,使矩形的顶点B落在矩形的边AD上,记该点为E,且折痕MN的两端点M、N分别位于边AB,BC上,设∠MNB=θ,MN=l,△EMN的面积为S,
已知矩形纸片ABCD中,AB=6,AD=12,将举行制品的右下角沿线段MN折叠,使矩形的顶点B落在矩形的边AD上,记该点为E,且折痕MN的两端点M、N分别位于边AB,BC上,设∠MNB=θ,MN=l,△EMN的面积为S,