题目内容
已知函数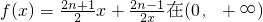 上的最小值是an(n∈N*).
上的最小值是an(n∈N*).
(1)求数列{an}的通项公式;
(2)证明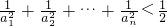 ;
;
(3)在点列An(2n,an)中,是否存在两点Ai,Aj(i,j∈N*)使直线AiAj的斜率为1?若存在,求出所有数对(i,j),若不存在,说明理由.
解:(1)∵ …(2分)
…(2分)
当且仅当
即 时,
时,
f(x)取得最小值 ,
,
∴ .…(4分)
.…(4分)
(2)证明∵ ,…(6分)
,…(6分)
∴
= .…(9分)
.…(9分)
(3)不存在.
设Ai(2i,ai),A(2j,aj),(其中i,j∈N*),
则 …(10分)
…(10分)
= …(12分)
…(12分)
= .
.
故不存在存在两点Ai,Aj(i,j∈N*)使直线AiAj的斜率为1.…(14分)
分析:(1)由 ,知当且仅当
,知当且仅当 时,f(x)取得最小值,由此能求出数列{an}的通项公式.
时,f(x)取得最小值,由此能求出数列{an}的通项公式.
(2)由 ,能够证明
,能够证明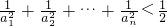 .
.
(3)设Ai(2i,ai),A(2j,aj),则 =
= =
= .故不存在存在两点Ai,Aj(i,j∈N*)使直线AiAj的斜率为1.
.故不存在存在两点Ai,Aj(i,j∈N*)使直线AiAj的斜率为1.
点评:本题考查数列与不等式的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
 …(2分)
…(2分)当且仅当

即
 时,
时,f(x)取得最小值
 ,
,∴
 .…(4分)
.…(4分)(2)证明∵
 ,…(6分)
,…(6分)∴

=
 .…(9分)
.…(9分)(3)不存在.
设Ai(2i,ai),A(2j,aj),(其中i,j∈N*),
则
 …(10分)
…(10分)=
 …(12分)
…(12分)=
 .
.故不存在存在两点Ai,Aj(i,j∈N*)使直线AiAj的斜率为1.…(14分)
分析:(1)由
 ,知当且仅当
,知当且仅当 时,f(x)取得最小值,由此能求出数列{an}的通项公式.
时,f(x)取得最小值,由此能求出数列{an}的通项公式.(2)由
 ,能够证明
,能够证明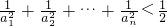 .
.(3)设Ai(2i,ai),A(2j,aj),则
 =
= =
= .故不存在存在两点Ai,Aj(i,j∈N*)使直线AiAj的斜率为1.
.故不存在存在两点Ai,Aj(i,j∈N*)使直线AiAj的斜率为1.点评:本题考查数列与不等式的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
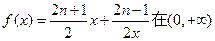 上的最小值是
上的最小值是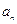 (
(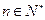 ).
).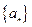 的通项公式;
的通项公式;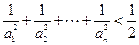 ;
;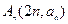 中,是否存在两点
中,是否存在两点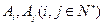 使直线
使直线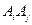 的斜率为1?若存在,求出所有数对
的斜率为1?若存在,求出所有数对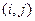 ,若不存在,说明理由.
,若不存在,说明理由.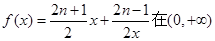 上的最小值是
上的最小值是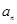 (
(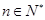 ).
).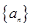 的通项公式;
的通项公式; ;
;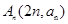 中,是否存在两点
中,是否存在两点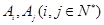 使直线
使直线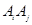 的斜率为1?若存在,求出所有数对
的斜率为1?若存在,求出所有数对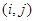 ,若不存在,说明理由.
,若不存在,说明理由.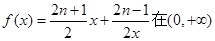 上的最小值是
上的最小值是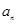 (
(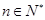 ).
).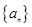 的通项公式;
的通项公式;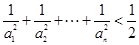 ;
;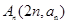 中,是否存在两点
中,是否存在两点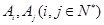 使直线
使直线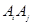 的斜率为1?若存在,求出所有数对
的斜率为1?若存在,求出所有数对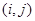 ,若不存在,说明理由.
,若不存在,说明理由.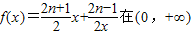 上的最小值是an(n∈N*).
上的最小值是an(n∈N*).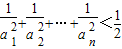 ;
;