题目内容
已知函数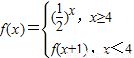 ,则f(2+log23)的值为( )
,则f(2+log23)的值为( )A.
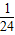
B.
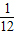
C.

D.

【答案】分析:先判断出2+log23<4,代入f(x+1)=f(3+log23),又因3+log23>4代入f(x)=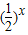 ,利用指数幂的运算性质求解.
,利用指数幂的运算性质求解.
解答:解:∵1<log23<2,∴3<2+log23<4,
∴f(2+log23)=f(2+log23+1)=f(3+log23),
∵4<3+log23<5,∴f(3+log23)=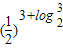 =
= ×
×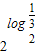 =
=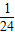 ,
,
故选A.
点评:本题的考点是分段函数求函数值,先判断自变量的范围,再代入对应的关系式,根据指数幂的运算性质进行化简求值.
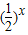 ,利用指数幂的运算性质求解.
,利用指数幂的运算性质求解.解答:解:∵1<log23<2,∴3<2+log23<4,
∴f(2+log23)=f(2+log23+1)=f(3+log23),
∵4<3+log23<5,∴f(3+log23)=
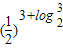 =
= ×
×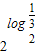 =
=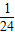 ,
,故选A.
点评:本题的考点是分段函数求函数值,先判断自变量的范围,再代入对应的关系式,根据指数幂的运算性质进行化简求值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,则f(2)= ;若f(x)=6,则x= .
,则f(2)= ;若f(x)=6,则x= . ,则f(2)= ;若f(x)=6,则x= .
,则f(2)= ;若f(x)=6,则x= . ,则f(2)= ;若f(x)=6,则x= .
,则f(2)= ;若f(x)=6,则x= . ,则f(2)=( )
,则f(2)=( ) ,则f(2)= ;若f(x)=6,则x= .
,则f(2)= ;若f(x)=6,则x= .