Question

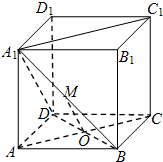如图，在正方体ABCD-A₁B₁C₁D₁中，O是底面正方形ABCD的中心，M是线段A₁B的中点．
（Ⅰ）证明：平面A₁BD⊥平面A₁ACC₁；
（Ⅱ）证明：MO∥平面B₁BCC₁．

Answer 1

分析：（Ⅰ）利用底面ABCD是正方形，说明BD⊥AC，然后证明BD⊥平面A₁ACC₁，推出平面A₁BD⊥平面A₁ACC₁． 
（Ⅱ）连接B₁C．证明MO∥A₁D．证明四边形A₁ DC B₁为平行四边形．即可证明A₁D∥B₁C．然后证明MO∥平面B₁BCC₁．

解答：满分（14分）．
证明：（Ⅰ）∵底面ABCD是正方形，
∴BD⊥AC．                             …（2分）
∵C₁C⊥底面ABCD，BD?底面ABCD，
∴BD⊥C₁C．
∵AC?平面A₁ACC₁，C₁C?平面A₁ACC₁，且
AC∩C₁C=C，
∴BD⊥平面A₁ACC₁．                    …（5分）
∵BD?平面A₁BD，
∴平面A₁BD⊥平面A₁ACC₁．            …（7分）
（Ⅱ）连B₁C．                            …（9分）
在△A₁BD中，∵O是BD的中点，M是BA₁的中点，
∴MO∥A₁D．                                                                      …（10分）
∵A₁ B₁∥DC，且A₁ B₁=DC，
∴四边形A₁ DC B₁为平行四边形．
∴A₁D∥B₁C．                                                                      …（12分）
∴MO∥B₁C，且B₁C?平面B₁BCC₁，MO?平面B₁BCC₁，
∴MO∥平面B₁BCC₁．                                                              …（14分）
说明：直线在平面内，既可用符号“”表示，也可用符号“?”表示，而且应特别让学生知道后一种表示．

点评：本小题主要考查空间线面关系，考查直线与平面平行与平面与平面的垂直，考查空间想像能力和推理论证能力．