题目内容
在△AOB中，已知点O（0，0），A（0，5），B（4，3），
=
，
=
，AD与BC交于点M，求点M的坐标．
| OC |
| 1 |
| 4 |
| OA |
| OD |
| 1 |
| 2 |
| OB |
分析：根据向量线性运算坐标公式，算出C（0，
）、（2，
），从而算出直线BC、AD的方程，最后联解所得方程，即可得到AD与BC交点M的坐标．
| 5 |
| 4 |
| 3 |
| 2 |
解答：解：∵O（0，0），A（0，5），
=
，
∴设点C（x1，y1），可得（x1，y1）=
（0，5），
解之得x1=0，y1=
，即C（0，
）
同理，可得点D坐标为（2，
）
由此可得直线AD方程为
=
，化简得y=-
x+5…①
同理，可得直线BC方程为y=
x+
…②
联解①②，得x=
，y=2，
即AD与BC交点M的坐标为（
，2）
| OC |
| 1 |
| 4 |
| OA |
∴设点C（x1，y1），可得（x1，y1）=
| 1 |
| 4 |
解之得x1=0，y1=
| 5 |
| 4 |
| 5 |
| 4 |
同理，可得点D坐标为（2，
| 3 |
| 2 |
由此可得直线AD方程为
| y-5 | ||
|
| x-0 |
| 2-0 |
| 7 |
| 4 |
同理，可得直线BC方程为y=
| 7 |
| 16 |
| 5 |
| 4 |
联解①②，得x=
| 12 |
| 7 |
即AD与BC交点M的坐标为（
| 12 |
| 7 |
点评：本题给出平面坐标系中向量满足的等式，求直线AD与BC交点M的坐标．着重考查了平面向量的线性运算的坐标表示、直线的方程与位置关系等知识，属于基础题．
练习册系列答案
相关题目
=
，
=
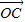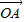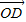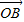，AD与BC交于点M，求点M的坐标．