题目内容
设函数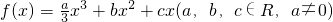 .
.
(1)若函数f(x)为奇函数,求b的值;
(2)在(1)的条件下,若a=-3,函数f(x)在[-2,2]上的值域为[-2,2],求f(x)的零点;
(3)若不等式axf'(x)≤f(x)+1恒成立,求a+b+c的取值范围.
解:(1)∵函数f(x)为奇函数,∴f(-x)=-f(x),解得b=0.
(2)由(1)可知f(x)=-x3+cx,∴f′(x)=-3x2+c.
①若c≤0,则f′(x)≤0恒成立,则f(x)单调递减,
又函数f(x)在[-2,2]上的值域为[-2,2],∴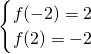 ,此方程无解.
,此方程无解.
②若c>0,则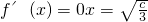
(ⅰ)若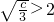 ,即c>12时,函数f(x)在[-2,2]上单调递增,∴
,即c>12时,函数f(x)在[-2,2]上单调递增,∴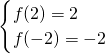 ,此方程组无解;
,此方程组无解;
(ⅱ)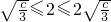 时,即3≤c≤12时,∴
时,即3≤c≤12时,∴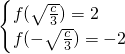 ,所以c=3;
,所以c=3;
(ⅲ)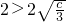 时,即c<3时,∴
时,即c<3时,∴ ,此方程组无解.
,此方程组无解.
综上可得c=3,∴f(x)=-x3+3x的零点为: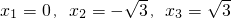 .
.
(3)由题设得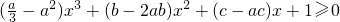 恒成立.
恒成立.
记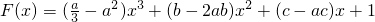 ,
,
若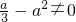 ,则三次函数F(x)至少有一个零点x0,且在x0左右两侧异号,
,则三次函数F(x)至少有一个零点x0,且在x0左右两侧异号,
所以原不等式不能恒成立;
所以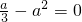 ,∴
,∴ ,此时
,此时 恒成立等价于:10.b=c=0或者20.
恒成立等价于:10.b=c=0或者20.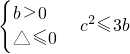
在10中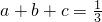
在20中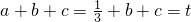 ,所以c2≤3t-3c-1?3t≥c2+3c+1,∴
,所以c2≤3t-3c-1?3t≥c2+3c+1,∴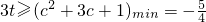
综上a+b+c的取值范围是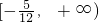 . …
. …
分析:(1)由题意可得f(-x)=-f(x),解之可得b=0;
(2)可得f(x)=-x3+cx,f′(x)=-3x2+c,结合导数的正负对函数单调性的影响,分c≤0,和c>0,两类进行讨论可得答案;
(3)推理可得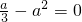 ,∴
,∴ ,此时
,此时 恒成立等价于:10.b=c=0或者20.
恒成立等价于:10.b=c=0或者20.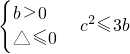 ,分别求解a+b+c的取值范围,综合可得.
,分别求解a+b+c的取值范围,综合可得.
点评:本题考查函数的奇偶性,和函数的恒成立问题,属中档题.
(2)由(1)可知f(x)=-x3+cx,∴f′(x)=-3x2+c.
①若c≤0,则f′(x)≤0恒成立,则f(x)单调递减,
又函数f(x)在[-2,2]上的值域为[-2,2],∴
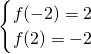 ,此方程无解.
,此方程无解.②若c>0,则
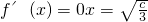
(ⅰ)若
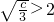 ,即c>12时,函数f(x)在[-2,2]上单调递增,∴
,即c>12时,函数f(x)在[-2,2]上单调递增,∴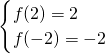 ,此方程组无解;
,此方程组无解;(ⅱ)
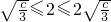 时,即3≤c≤12时,∴
时,即3≤c≤12时,∴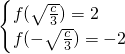 ,所以c=3;
,所以c=3;(ⅲ)
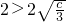 时,即c<3时,∴
时,即c<3时,∴ ,此方程组无解.
,此方程组无解.综上可得c=3,∴f(x)=-x3+3x的零点为:
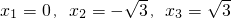 .
.(3)由题设得
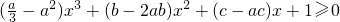 恒成立.
恒成立.记
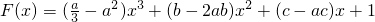 ,
,若
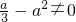 ,则三次函数F(x)至少有一个零点x0,且在x0左右两侧异号,
,则三次函数F(x)至少有一个零点x0,且在x0左右两侧异号,所以原不等式不能恒成立;
所以
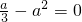 ,∴
,∴ ,此时
,此时 恒成立等价于:10.b=c=0或者20.
恒成立等价于:10.b=c=0或者20.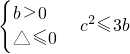
在10中
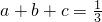
在20中
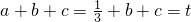 ,所以c2≤3t-3c-1?3t≥c2+3c+1,∴
,所以c2≤3t-3c-1?3t≥c2+3c+1,∴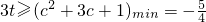
综上a+b+c的取值范围是
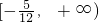 . …
. …分析:(1)由题意可得f(-x)=-f(x),解之可得b=0;
(2)可得f(x)=-x3+cx,f′(x)=-3x2+c,结合导数的正负对函数单调性的影响,分c≤0,和c>0,两类进行讨论可得答案;
(3)推理可得
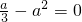 ,∴
,∴ ,此时
,此时 恒成立等价于:10.b=c=0或者20.
恒成立等价于:10.b=c=0或者20.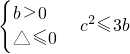 ,分别求解a+b+c的取值范围,综合可得.
,分别求解a+b+c的取值范围,综合可得.点评:本题考查函数的奇偶性,和函数的恒成立问题,属中档题.

练习册系列答案
相关题目
 ,
,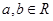
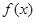 在
在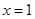 处与直线
处与直线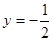 相切;
相切;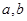 的值;②求函数
的值;②求函数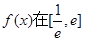 上的最大值;
上的最大值;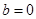 时,若不等式
时,若不等式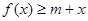 对所有的
对所有的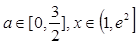 都成立,求实数
都成立,求实数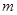 的取值范围.
的取值范围. ,
,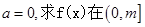
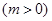 上的最大值
上的最大值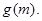
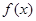 在区间[1,2]上为减函数,求a的取值范围。
在区间[1,2]上为减函数,求a的取值范围。 为函数
为函数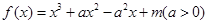 .
.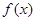 在
在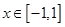 内没有极值点,求实数
内没有极值点,求实数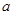 的取值范围;
的取值范围;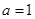 时函数
时函数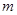 的取值范围;
的取值范围;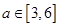 ,不等式
,不等式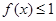 在
在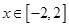 上恒成立,求实数
上恒成立,求实数 ,
, 与函数
与函数 ,
, 的图像都相切,且与函数
的图像都相切,且与函数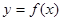 在其定义域内为单调函数,求实数P的取值范围
在其定义域内为单调函数,求实数P的取值范围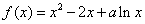 。
。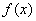 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数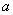 的取值范围;
的取值范围;