题目内容
已知函数![]() .
.
(I)将![]() 写成
写成![]() 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(II)如果△ABC的三边a、b、c满足b2= a c,且边b所对的角为![]() ,试求
,试求![]() 的范围及此时函数
的范围及此时函数![]() 的值域.
的值域.
(I)对称中心的横坐标为![]() ,(k∈Z).
,(k∈Z).
(II)0<x≤![]() . f(x)的值域为(2
. f(x)的值域为(2![]() ,1+
,1+![]() ).
).
解析:
(I)f(x) =![]() +
+![]() (1+
(1+![]() )=
)=![]() +
+![]()
![]() +
+![]()
=sin(![]() +
+![]() )+
)+![]() .由sin(
.由sin(![]() +
+![]() )= 0,即
)= 0,即![]() +
+![]() =kπ(k∈Z),
=kπ(k∈Z),
得x=![]() (k∈Z),即对称中心的横坐标为
(k∈Z),即对称中心的横坐标为![]() ,(k∈Z).
,(k∈Z).
(II)由已知b2=ac,得cosx=![]() ≥
≥![]() .
.
∴![]() ≤cosx<1,0<x≤
≤cosx<1,0<x≤![]() .
.
∴![]() <
<![]() +
+![]() ≤
≤![]() .∵
.∵![]() >
>![]() ,
,
∴sin![]() <sin(
<sin(![]() +
+![]() )≤1.
)≤1. ![]() +
+![]() <sin(
<sin(![]() +
+![]() )+
)+![]() ≤1+
≤1+![]() ,
,
即f(x)的值域为(2![]() ,1+
,1+![]() ).
).

练习册系列答案
相关题目
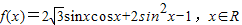 .
. ,再把所得到的图象向左平移
,再把所得到的图象向左平移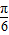 个单位长度,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位长度,得到函数y=g(x)的图象,求函数y=g(x)在区间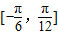 上的值域.
上的值域.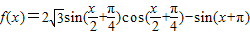 .
.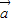 =(
=(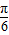 ,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. =(
=( ,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.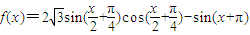 .
.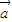 =(
=(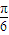 ,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.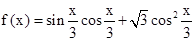 .
.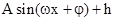 (
(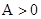 )的形式,并求其图像对称中心的横坐标;
)的形式,并求其图像对称中心的横坐标;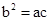 ,且边b所对的角为B,试求角B的取值范围及此时函数f(B)的值域.
,且边b所对的角为B,试求角B的取值范围及此时函数f(B)的值域.