题目内容
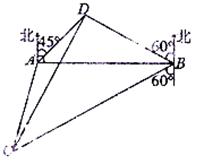
(满分12分)如图,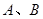 是海面上位于东西方向相距
是海面上位于东西方向相距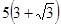 海里的两个观测点,现位于
海里的两个观测点,现位于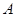 点北偏东
点北偏东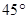 ,
,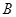 点北偏西
点北偏西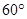 的
的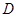 点有一艘轮船发出求救信号,位于
点有一艘轮船发出求救信号,位于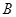 点南偏西
点南偏西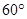 °且与
°且与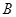 点相距
点相距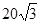 海里的
海里的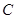 点的救援船立即即前往营救,其航行速度为
点的救援船立即即前往营救,其航行速度为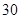 海里/小时,该救援船到达
海里/小时,该救援船到达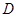 点需要多长时间?
点需要多长时间?
【答案】
该救援船到达 点需要1小时。
点需要1小时。
【解析】本题考查了正弦定理与余弦定理.准确找出题中的方向角是解题的关键之处.
在△DAB中,由正弦定理得DB:sin∠DAB =AB: sin∠ADB ,由此可以求得DB=10 3
海里;然后在△DBC中,由余弦定理得CD2=BD2+BC2-2BD•BC•cos∠DBC=900,即CD=30海里;最后根据时间=路程 :速度 即可求得该救援船到达D点需要的时间.
解 由题意知 =
= 海里,
海里,
∠ DBA=90°—60°=30°,∠ DAB=90°—45°=45°,……2分
∴∠ADB=180°—(45°+30°)=105°,……3分
在△ADB中,有正弦定理得 ……5分
……5分

即 ……7分
……7分
在△BCD中,有余弦定理得:
 ……9分
……9分
=
=900
即 海里……10分
海里……10分
设所需时间为 小时,则
小时,则 小时……11分
小时……11分
答:该救援船到达 点需要1小时……12分
点需要1小时……12分

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段 的中点
的中点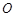 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线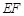 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.
 中,
中, ,
, ,
, ,平面
,平面 平面
平面 ,
, 是线段
是线段 上一点,
上一点, ,
, ,
, .
. 平面
平面 ;
; 与四棱锥
与四棱锥 与
与 ,求
,求 的值.
的值.

 的中点,P为BB1的中点.
的中点,P为BB1的中点. ;
; 所成角的大小;
所成角的大小;