Question

观察下列各不等式：

1+＜，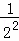

1++＜，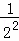

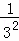1+++＜，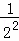

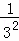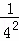1++++＜，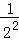

…

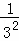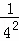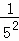（1）由上述不等式，归纳出一个与正整数n（n≥2）有关的一般性结论；

（2）用数学归纳法证明你得到是结论．

　

Answer 1

解：（1）观察1+＜，

1++＜，

1+++＜，

1++++＜，

…

各不等式，得到与正整数n有关的一般不等式为

1++++＜且n≥2．…（6分）

（2）以下用数学归纳法证明这个不等式．

①当n=2时，由题设可知，不等式显然成立．

②假设当n=k时，不等式成立，即

 1++++＜              …（8分）

那么，当n=k+1时，有 1+++++＜

===．

所以当n=k+1时，不等式也成立．…（14分）

根据①和②，可知不等式对任何n∈N₊且n≥2都成立．…（16分）