题目内容
(本小题满分12分)
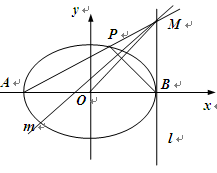
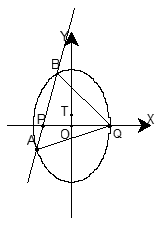
如图,在平面直角坐标系 中,椭圆
中,椭圆 的焦距为2,且过点
的焦距为2,且过点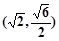 .
.
求椭圆 的方程;
的方程;
若点 ,
, 分别是椭圆
分别是椭圆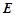 的左、右顶点,直线
的左、右顶点,直线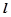 经过点
经过点 且垂直于
且垂直于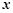 轴,点
轴,点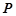 是椭圆上异于
是椭圆上异于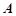 ,
, 的任意一点,直线
的任意一点,直线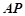 交
交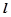 于点
于点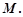
(ⅰ)设直线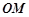 的斜率为
的斜率为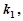 直线
直线 的斜率为
的斜率为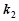 ,求证:
,求证: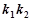 为定值;
为定值;
(ⅱ)设过点 垂直于
垂直于 的直线为
的直线为 .求证:直线
.求证:直线 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
(1)见解析 (2)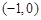
解析试题分析:⑴由题意得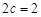 ,所以
,所以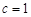 ,又
,又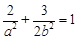 ,
,
消去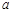 可得,
可得,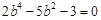 ,解得
,解得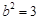 或
或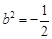 (舍去),则
(舍去),则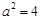 ,
,
所以椭圆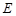 的方程为
的方程为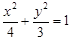 .
.
⑵(ⅰ)设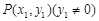 ,
,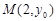 ,则
,则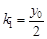 ,
,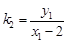 ,
,
因为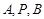 三点共线,所以
三点共线,所以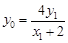 ,所以,
,所以,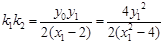 ,8分
,8分
因为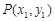 在椭圆上,所以
在椭圆上,所以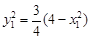 ,故
,故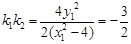 为定值.10分
为定值.10分
(ⅱ)直线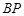 的斜率为
的斜率为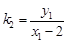 ,直线
,直线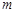 的斜率为
的斜率为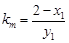 ,
,
则直线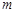 的方程为
的方程为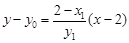 ,
,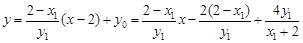
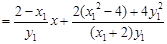
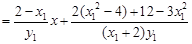 =
=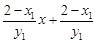 =
=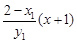 ,
,
所以直线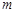 过定点
过定点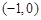 .
.
考点:直线的斜率;恒过定点的直线;直线与椭圆的位置关系
点评:本题考查转化的技巧,(1)将两斜率之积为定值的问题转化成了两根之积来求,(2)中将求两动点的连线过定点的问题转化成了求直线系过定点的问题,转化巧妙,有艺术性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的右焦点为
的右焦点为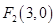 ,离心率为
,离心率为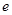 。
。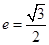 ,求椭圆的方程。
,求椭圆的方程。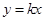 与椭圆相交于
与椭圆相交于 两点,
两点,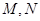 分别为线段
分别为线段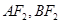 的中点。若坐标原点
的中点。若坐标原点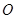 在以线段
在以线段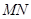 为直径的圆上,且
为直径的圆上,且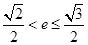 ,求
,求 的取值范围。
的取值范围。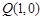 在椭圆C:
在椭圆C: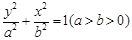 上,且椭圆C的离心率
上,且椭圆C的离心率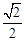 .
.
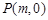 作直线交椭圆C于点A.B.△ABQ的垂心为T,是否存在实数m ,使得垂心T在y轴上.若存在,求出实数m的取值范围;若不存在,请说明理由.
作直线交椭圆C于点A.B.△ABQ的垂心为T,是否存在实数m ,使得垂心T在y轴上.若存在,求出实数m的取值范围;若不存在,请说明理由. ,曲线
,曲线 上任一点
上任一点 满足
满足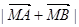 =
=
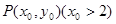 是(1)中所求曲线
是(1)中所求曲线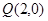 ,线段
,线段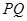 的垂直平分线与
的垂直平分线与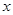 轴交于点
轴交于点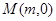 ,求实数
,求实数 的最小值.
的最小值.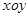 中,点
中,点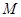 到两定点F1
到两定点F1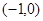 和F2
和F2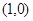 的距离之和为
的距离之和为 ,设点
,设点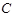 .(1)求曲线
.(1)求曲线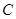 的方程; (2)若直线
的方程; (2)若直线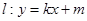 与曲线
与曲线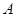 、
、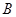 (
(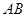 为直径的圆过点
为直径的圆过点 ,试判断直线
,试判断直线 是否经过一定点,若是,求出定点坐标;若不是,说明理由.
是否经过一定点,若是,求出定点坐标;若不是,说明理由.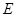 的中心在坐标原点、对称轴为坐标轴,且抛物线
的中心在坐标原点、对称轴为坐标轴,且抛物线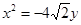 的焦点是它的一个焦点,又点
的焦点是它的一个焦点,又点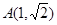 在该椭圆上.
在该椭圆上.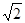 直线
直线 与椭圆
与椭圆 ,当
,当 面积的最大值时,求直线
面积的最大值时,求直线 的离心率为
的离心率为 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 .
. 的方程;
的方程; 与椭圆
与椭圆 两点,坐标原点
两点,坐标原点 到直线
到直线 ,求
,求
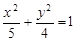 的右焦点
的右焦点 重合,过点
重合,过点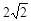 的直线与抛物线交于
的直线与抛物线交于 ,
, 两点.
两点.
 的面积.
的面积. +
+ =1(a>b>0)的一个焦点是F(1,0),且离心率为
=1(a>b>0)的一个焦点是F(1,0),且离心率为 .
.