题目内容
若复数x+3-yi与2+xi互为共轭复数,x,y∈R,则|y+xi|=( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
分析:由复数x+3-yi与2+xi互为共轭复数,则它们的实部相等,虚部互为相反数,由此列式求出x,y的值,则|y+xi|可求.
解答:解:∵x,y∈R,且复数x+3-yi与2+xi互为共轭复数,
则
,解得:
,
∴|y+xi|=|-1-i|=
=
.
故选:B.
则
|
|
∴|y+xi|=|-1-i|=
| (-1)2+(-1)2 |
| 2 |
故选:B.
点评:本题考查了复数的基本概念,考查了复数相等的条件及复数模的求法,是基础的计算题.

练习册系列答案
相关题目
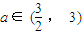 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点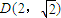 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;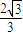 ,求实数x的取值范围.
,求实数x的取值范围.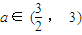 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点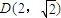 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;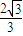 ,求实数x的取值范围.
,求实数x的取值范围.