题目内容
如图，在△ABC中，AD=2DB，AE=3EC，CD与BE交于F，设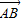
=
，
=
，
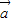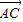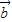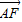=x
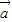+y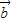
，则（x，y）为（ ）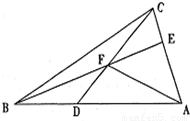
A．
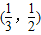
B．
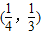
C．
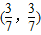
D．
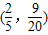
【答案】分析：根据AD=2DB，AE=3EC，利用B、F、E三点共线和C、F、D三点共线分别表示出向量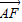
，根据平面向量基本定理可求出x、y的值．
解答：解：∵AD=2DB，AE=3EC
∴
，
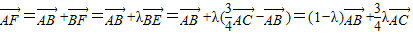同理向量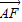
还可以表示为
，
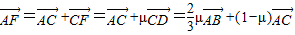根据平面向量基本定理可知向量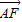
用不共线的两个向量线性表示是唯一的
则对应系数相等可得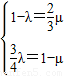
解得
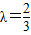，所以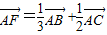
，
故选A．
点评：本题主要考查了平面向量的基本定理及其意义，同时考查了分析问题的能力和计算能力，属于基础题．
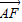，根据平面向量基本定理可求出x、y的值．解答：解：∵AD=2DB，AE=3EC
∴
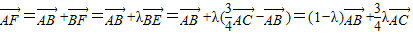，同理向量
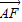还可以表示为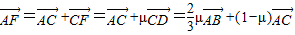，根据平面向量基本定理可知向量
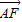用不共线的两个向量线性表示是唯一的则对应系数相等可得
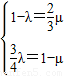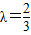解得，所以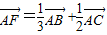，故选A．
点评：本题主要考查了平面向量的基本定理及其意义，同时考查了分析问题的能力和计算能力，属于基础题．
练习册系列答案
字词句段篇系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知