题目内容
点M(a,b)在由不等式组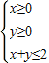 确定的平面区域内,则点N(a+b,a-b)所在平面区域的面积是 .
确定的平面区域内,则点N(a+b,a-b)所在平面区域的面积是 .
【答案】分析:设m=a+b,n=a-b,则N(a+b,a-b)为N(m,n),由M(a,b)满足的不等式组,化简整理得到m、n满足的不等式组,最后以m为横坐标、n为纵坐标,直角坐标系内作出相应的平面区域,即可求出点N(a+b,a-b)所在平面区域的面积.
解答:解:由M(a,b)满足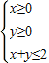 ,可得
,可得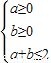
令m=a+b,n=a-b,则N(a+b,a-b)为N(m,n)
解得 2a=m+n,2b=m-n
因为a≥0,b≥0,且a+b≤2
∴N(m,n)满足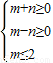
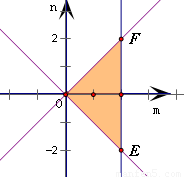
以m为横坐标,n为纵坐标,在直角坐标系中画出不等式组表示的平面区域如图,
得到△OEF,其中O(0,0),E(2,2),F(2,-2),
可得S△OEF= ×EF×2=4.
×EF×2=4.
即得N(a+b,a-b)所在平面区域的面积是4
故答案为:4
点评:本题给出M(a,b)满足的不等式组,求点N(a+b,a-b)所在平面区域的面积,着重考查了坐标变换公式和简单的性质规划及其应用等知识,属于基础题.
解答:解:由M(a,b)满足
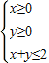 ,可得
,可得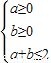

令m=a+b,n=a-b,则N(a+b,a-b)为N(m,n)
解得 2a=m+n,2b=m-n
因为a≥0,b≥0,且a+b≤2
∴N(m,n)满足
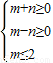
以m为横坐标,n为纵坐标,在直角坐标系中画出不等式组表示的平面区域如图,
得到△OEF,其中O(0,0),E(2,2),F(2,-2),
可得S△OEF=
 ×EF×2=4.
×EF×2=4.即得N(a+b,a-b)所在平面区域的面积是4
故答案为:4
点评:本题给出M(a,b)满足的不等式组,求点N(a+b,a-b)所在平面区域的面积,着重考查了坐标变换公式和简单的性质规划及其应用等知识,属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
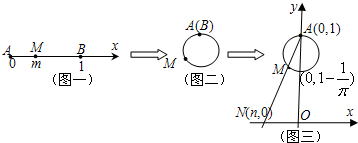 如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )
如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )(1)f(
| 1 |
| 2 |
(2)f(x)是偶函数;
(3)f(x)在其定义域上是增函数;
(4)y=f(x)的图象关于点(
| 1 |
| 2 |
| A、(1)(3)(4) |
| B、(1)(2)(3) |
| C、(1)(2)(4) |
| D、(1)(2)(3)(4) |
 确定的平面区域内,则点N(a+b,a-b)所在的平面区域的面积是 ( )
确定的平面区域内,则点N(a+b,a-b)所在的平面区域的面积是 ( )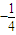 .
.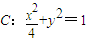 上;
上;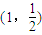 ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;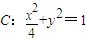 内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.
内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.