题目内容
已知向量a=(cosα,sinα),b=(cosx,sinx),c=(sinx+2sinα,cosx+2cosα),其中0<α<x<π。
(1)若 ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;
(2)若a与b的夹角为 ,且a⊥c,求tan2α的值。
,且a⊥c,求tan2α的值。
(1)若
 ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;(2)若a与b的夹角为
 ,且a⊥c,求tan2α的值。
,且a⊥c,求tan2α的值。解:(1)∵ b=(cosx,sinx),c=(sinx+2sinα,cosx+2cosα),
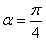
∴f(x)=b·c=cosxsinx+2cosxsinα+sinxcosx+2sinxcosα
=2sinxcosx+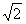 (sinx+cosx)
(sinx+cosx)
令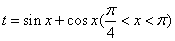
则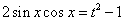 ,且
,且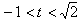
则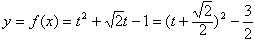 ,
,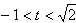
所以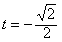 ,
,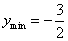
此时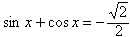
由于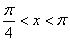 ,故
,故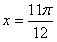
所以函数f(x)的最小值为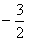 ,相应x的值为
,相应x的值为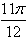 。
。
(2)∵a与b的夹角为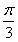
∴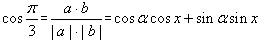
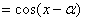
∵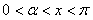
∴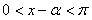
∴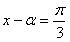
∵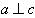
∴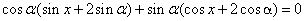
∴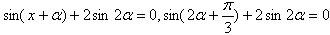
∴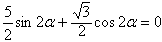
∴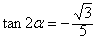 。
。
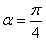
∴f(x)=b·c=cosxsinx+2cosxsinα+sinxcosx+2sinxcosα
=2sinxcosx+
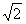 (sinx+cosx)
(sinx+cosx)令
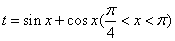
则
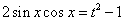 ,且
,且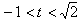
则
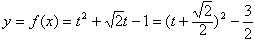 ,
,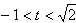
所以
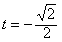 ,
,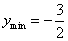
此时
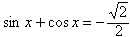
由于
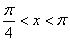 ,故
,故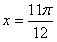
所以函数f(x)的最小值为
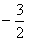 ,相应x的值为
,相应x的值为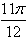 。
。(2)∵a与b的夹角为
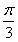
∴
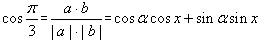
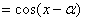
∵
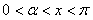
∴
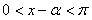
∴
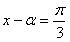
∵
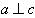
∴
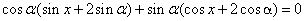
∴
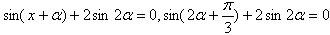
∴
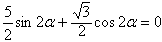
∴
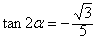 。
。
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目