Question

设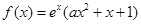，且曲线y＝f（x）在x＝1处的切线与x轴平行。

（Ⅰ）求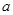的值，并讨论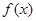的单调性；

（Ⅱ）证明：当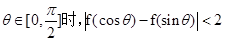

 

Answer 1

【答案】

（Ⅰ）函数的增区间为   减区间为

（Ⅱ）见解析

【解析】本试题主要考查了导数在研究函数中的运用。利用导数来判定函数单调性和研究函数的最值的综合运用。（1）利用，且曲线y＝f（x）在x＝1处的切线与x轴平行，求解得到参数a的值，然后代入函数式中求解导数大于零或者小于零的解集，得到结论。

（2）在第一问的基础上，根据在单调增加，故在的最大值为

最小值为，从而证明即可。显然成立

解：（Ⅰ） 

由题知：        所以  ＝－1　　    ………2分

此时：

所以函数的增区间为   减区间为 ………5分

（Ⅱ）由（Ⅰ）知在单调增加，故在的最大值为，

最小值为

从而对任意，，有

而当时，   从而