题目内容
数列![]() 的前
的前![]() 项和
项和![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() 且
且![]()
(1)求数列![]() 与
与![]() 的通项公式.
的通项公式.
(2)设数列![]() 满足
满足![]() ,其前
,其前![]() 项和为
项和为![]() ,求
,求![]()
解: (1)对于数列![]() 有
有![]() ①
①
![]() ②
②
由①- ②得![]() ,
,
![]() ,
,
则![]() ;
;
对于数列![]() 有:
有:![]() 可得
可得![]() .
.
(2)由(1)可知: ![]()
![]() =
=![]()
3![]() =
=![]()
-2![]() =
=![]()
=![]()
则![]() =
=![]()

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
(本小题满分14分)
已知函数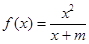 的图像经过点
的图像经过点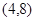 .
.
(1)求该函数的解析式;
(2)数列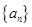 中,若
中,若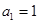 ,
,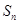 为数列
为数列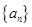 的前
的前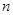 项和,且满足
项和,且满足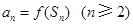 ,
,
证明数列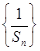 成等差数列,并求数列
成等差数列,并求数列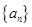 的通项公式;
的通项公式;
(3)另有一新数列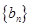 ,若将数列
,若将数列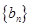 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
|
|
|
|
|
|
|
|
记表中的第一列数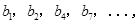 构成的数列即为数列
构成的数列即为数列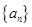 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
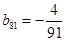 时,求上表中第
时,求上表中第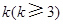 行所有项的和.
行所有项的和.
 ,写出
,写出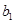
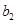
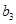
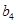
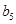
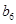
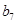
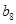
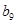
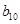
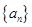 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表: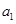
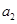
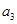
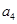
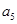
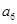
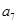
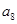
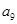
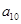
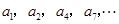 构成的数列为
构成的数列为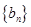 ,
,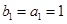 .
.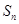 为数列
为数列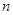 项和,且满足
项和,且满足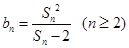 .
.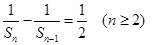 ;
;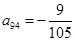 时,求上表中第
时,求上表中第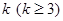 行所有项的和.
行所有项的和. 中的所有项按每一行比上一行多一项的规则排成下表:
中的所有项按每一行比上一行多一项的规则排成下表:









 ,
, ,
, 为数列
为数列 项和,且满足
项和,且满足
 成等差数列,并求数列
成等差数列,并求数列 时,求上表中第
时,求上表中第 行所有项的和
行所有项的和