题目内容

在平行六面体ABCD-A1B1C1D1中，设
AC1
=x
AB
+2y
BC
+3z
CC1
，则x+y+z等于（　　）
A、1
B、
2
3
C、
5
6
D、
11
6
分析：在平行六面体ABCD-A1B1C1D1中，用
AB
、
BC
、
CC1
 表示出
AC1
，将它和题中已知的
AC1
 的解析式作对照，
求出x、y、z 的值．
解答：解：∵在平行六面体ABCD-A1B1C1D1中，
AC1
=x
AB
+2y
BC
+3z
CC1
，
又∵
AC1
=
AB
+
BC
+
CC1
，∴x=1，2y=1，3z=1，
∴x=1，y=
1
2
，z=
1
3
，∴x+y+z=1+
1
2
+
1
3
=
11
6
，
故选 D．
点评：本题考查空间向量基本定理及其意义，空间向量的加减和数乘运算，用待定系数法求出x、y、z 的值．
练习册系列答案
相关题目
如图，在平行六面体ABCD-A1B1C1D1中，O为AC与BD的交点，若
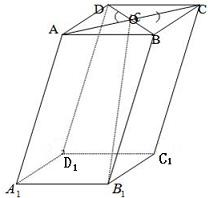
A1B1
=
a
，
A1D1
=
b
，
AA1
=
c
，则向量
B1O
等于（　　）
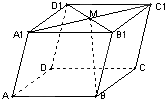精英家教网
A、
1
2
a
+
1
2
b
+
c
B、
1
2
a
-
1
2
b
+
c
C、-
1
2
a
+
1
2
b
+
c
D、-
1
2
a
-
1
2
b
+
c
精英家教网如图：在平行六面体ABCD-A1B1C1D1中，M为A1C1与B1D1的交点．若
AB
=
a
，
AD
=
b
，
AA1
=
c
，则下列向量中与
BM
相等的向量是（　　）
A、-
1
2
a
+
1
2
b
+
c
B、
1
2
a
+
1
2
b
+
c
C、-
1
2
a
-
1
2
b
+
c
D、
1
2
a-
1
2
b+c
在平行六面体ABCD-A1B1C1D1中，向量
D1A
、
D1C
、
A1C1
是（　　）
已知在平行六面体ABCD-A1B1C1D1中，AB=AD=AA1=1，且∠BAD=∠BAA1=∠DAA1=60°，求AC1的长．
在平行六面体ABCD-A1B1C1D1中，
AC
=
a
，
BD
=
b
，
AC1
=
c
，试用
a
、
b
、
c
表示
BD1
=
b
+
c
-
a
b
+
c
-
a
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网