题目内容
18.命题p:“a>1,b>1”是命题q:“(a-1)(b-1)>0”( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合不等式的性质进行判断即可.
解答 解:若(a-1)(b-1)>0,则a-1>0且b-1>0或a-1<0,b-1<0,
即a>1,b>1或a<1,b<1,
即p是q的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,结合不等式的关系是解决本题的关键.

练习册系列答案
相关题目
9.函数f(x)的定义域为[0,1),则f(1-3x)的定义域是( )
| A. | (-2,1] | B. | (-$\frac{1}{2}$,1] | C. | (0,$\frac{1}{3}$] | D. | (-$\frac{1}{3}$,0] |
3.设函数f(x)=sin(ωx+φ)(ω,φ是常数,ω>0,0<φ<π),若f(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上具有单调性,且f($\frac{π}{6}$)=-f($\frac{π}{3}$)=-f($\frac{π}{2}$),则f(π)的值为( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 1 |
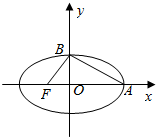 如图所示,椭圆中心在坐标原点,F为左焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,该椭圆被称为“黄金椭圆”,其离心率为$\frac{\sqrt{5}-1}{2}$,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$.
如图所示,椭圆中心在坐标原点,F为左焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,该椭圆被称为“黄金椭圆”,其离心率为$\frac{\sqrt{5}-1}{2}$,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$.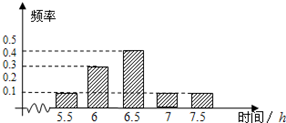 某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.
某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.