题目内容
(1)已知x>0,y>0,且 +
+ =1,求x+y的最小值;
=1,求x+y的最小值;(2)已知x<
 ,求函数y=4x-2+
,求函数y=4x-2+ 的最大值;
的最大值;(3)若x,y∈(0,+∞)且2x+8y-xy=0,求x+y的最小值;
(4)若-4<x<1,求
 的最大值.
的最大值.
【答案】分析:(1)利用 +
+ =1与x+y相乘,展开利用均值不等式求解即可.
=1与x+y相乘,展开利用均值不等式求解即可.
(2)由x< ,可得4x-5<0,首先应调整符号,再变形处理,即配凑积为定值.
,可得4x-5<0,首先应调整符号,再变形处理,即配凑积为定值.
(3)由2x+8y-xy=0变形可得 +
+ =1,与x+y相乘,展开利用均值不等式求解即可.
=1,与x+y相乘,展开利用均值不等式求解即可.
(4)先利用配方法和拆项法将原式变形, =
= •
• =
=
 ,再调整符号,利用均值不等式求解.
,再调整符号,利用均值不等式求解.
解答:解:(1)∵x>0,y>0, +
+ =1,∴x+y=(x+y)
=1,∴x+y=(x+y) =
= +
+ +10≥6+10=16.
+10≥6+10=16.
当且仅当 =
= 时,上式等号成立,又
时,上式等号成立,又 +
+ =1,∴x=4,y=12时,(x+y)min=16.
=1,∴x=4,y=12时,(x+y)min=16.
(2)∵x< ,∴5-4x>0,∴y=4x-2+
,∴5-4x>0,∴y=4x-2+ =-
=- +3≤-2+3=1,
+3≤-2+3=1,
当且仅当5-4x= ,即x=1时,上式等号成立,故当x=1时,ymax=1.
,即x=1时,上式等号成立,故当x=1时,ymax=1.
(3)由2x+8y-xy=0,得2x+8y=xy,∴ +
+ =1,
=1,
∴x+y=(x+y) =10+
=10+ +
+
=10+2 ≥10+2×2×
≥10+2×2× =18,
=18,
当且仅当 =
= ,即x=2y时取等号,
,即x=2y时取等号,
又2x+8y-xy=0,∴x=12,y=6,
∴当x=12,y=6时,x+y取最小值18.
(4) =
= •
• =
=

=-

∵-4<x<1,∴-(x-1)>0, >0.
>0.
从而 ≥2
≥2
-
 ≤-1
≤-1
当且仅当-(x-1)= ,
,
即x=2(舍)或x=0时取等号.
即 =-1.
=-1.
点评:利用基本不等式求函数最值是高考考查的重点内容,对不符合基本不等式形式的应首先变形,然后必须满足三个条件:一正、二定、三相等.同时注意灵活运用“1”的代换.
 +
+ =1与x+y相乘,展开利用均值不等式求解即可.
=1与x+y相乘,展开利用均值不等式求解即可.(2)由x<
 ,可得4x-5<0,首先应调整符号,再变形处理,即配凑积为定值.
,可得4x-5<0,首先应调整符号,再变形处理,即配凑积为定值.(3)由2x+8y-xy=0变形可得
 +
+ =1,与x+y相乘,展开利用均值不等式求解即可.
=1,与x+y相乘,展开利用均值不等式求解即可.(4)先利用配方法和拆项法将原式变形,
 =
= •
• =
=
 ,再调整符号,利用均值不等式求解.
,再调整符号,利用均值不等式求解.解答:解:(1)∵x>0,y>0,
 +
+ =1,∴x+y=(x+y)
=1,∴x+y=(x+y) =
= +
+ +10≥6+10=16.
+10≥6+10=16.当且仅当
 =
= 时,上式等号成立,又
时,上式等号成立,又 +
+ =1,∴x=4,y=12时,(x+y)min=16.
=1,∴x=4,y=12时,(x+y)min=16.(2)∵x<
 ,∴5-4x>0,∴y=4x-2+
,∴5-4x>0,∴y=4x-2+ =-
=- +3≤-2+3=1,
+3≤-2+3=1,当且仅当5-4x=
 ,即x=1时,上式等号成立,故当x=1时,ymax=1.
,即x=1时,上式等号成立,故当x=1时,ymax=1.(3)由2x+8y-xy=0,得2x+8y=xy,∴
 +
+ =1,
=1,∴x+y=(x+y)
 =10+
=10+ +
+
=10+2
 ≥10+2×2×
≥10+2×2× =18,
=18,当且仅当
 =
= ,即x=2y时取等号,
,即x=2y时取等号,又2x+8y-xy=0,∴x=12,y=6,
∴当x=12,y=6时,x+y取最小值18.
(4)
 =
= •
• =
=

=-


∵-4<x<1,∴-(x-1)>0,
 >0.
>0.从而
 ≥2
≥2-

 ≤-1
≤-1当且仅当-(x-1)=
 ,
,即x=2(舍)或x=0时取等号.
即
 =-1.
=-1.点评:利用基本不等式求函数最值是高考考查的重点内容,对不符合基本不等式形式的应首先变形,然后必须满足三个条件:一正、二定、三相等.同时注意灵活运用“1”的代换.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
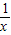 +
+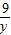 =2,求x+y的最小值.
=2,求x+y的最小值.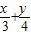 =1,求xy的最大值.
=1,求xy的最大值.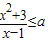 恒成立,求a的取值范围.
恒成立,求a的取值范围.