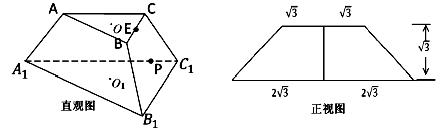题目内容
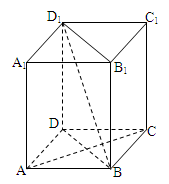
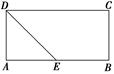
如图,在四棱锥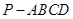 中,底面
中,底面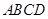 是矩形,侧棱
是矩形,侧棱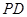 ⊥底面
⊥底面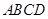 ,
,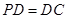 ,
,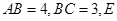 是
是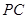 的中点,
的中点,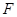 为
为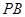 的中点.
的中点.
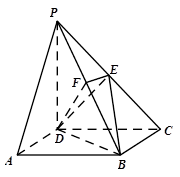
(1)证明: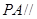 平面
平面
(2)若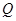 为直线
为直线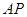 上任意一点,求几何体
上任意一点,求几何体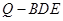 的体积;
的体积;
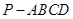 中,底面
中,底面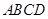 是矩形,侧棱
是矩形,侧棱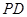 ⊥底面
⊥底面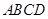 ,
,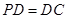 ,
,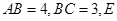 是
是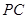 的中点,
的中点,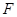 为
为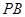 的中点.
的中点.
(1)证明:
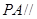 平面
平面
(2)若
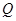 为直线
为直线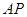 上任意一点,求几何体
上任意一点,求几何体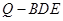 的体积;
的体积;(1)要证明线面平行,则利用判定定理,先证明 ∥
∥ ,然后根据判定定理得到证明。
,然后根据判定定理得到证明。
(2)4
 ∥
∥ ,然后根据判定定理得到证明。
,然后根据判定定理得到证明。(2)4
试题分析:
证明:(1)连结
 交
交 与
与 ,连结
,连结 .
.∵底面
 是正方形,∴点
是正方形,∴点 是
是 的中点.
的中点.又∵
 是
是 的中点∴在△
的中点∴在△ 中,
中, 为中位线 ∴
为中位线 ∴ ∥
∥ .
.而

 平面
平面 ,
,
 平面
平面 ,∴
,∴ ∥平面
∥平面 .
.(2)
 ∥平面
∥平面 ,
,
点评:主要是考查了空间几何体的体积和线面平行的证明,属于基础题。

练习册系列答案
相关题目
 是两个不同的平面,则下列四个命题中是真命题的是( )
是两个不同的平面,则下列四个命题中是真命题的是( )



 .
.
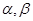 为两个不同的平面,下列四个命题中,其中正确的命题是 .(填写正确命题的序号)
为两个不同的平面,下列四个命题中,其中正确的命题是 .(填写正确命题的序号)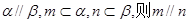 ;②若
;②若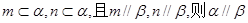 ;
;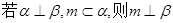 ;④
;④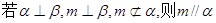
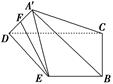
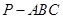 的底面
的底面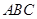 是直角三角形,且
是直角三角形,且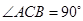 ,
,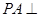 平面
平面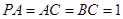 ,
,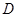 是线段
是线段 的中点,如图所示.
的中点,如图所示.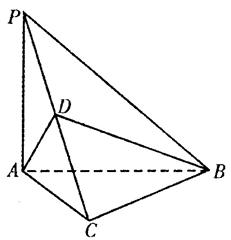
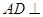 平面
平面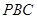 ;
;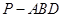 的体积.
的体积. 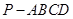 中,
中,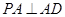 ,
,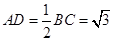 ,
,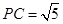 .
.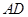 ∥
∥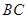 ,
,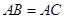 .
.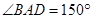
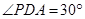 .
.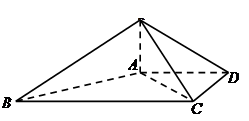
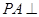 平面
平面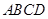 ;
;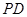 上是否存在一点
上是否存在一点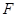 ,使直线
,使直线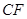 与平面
与平面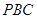 成角正弦值等于
成角正弦值等于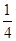 ,若存在,指出
,若存在,指出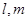 ,平面
,平面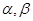 ,且
,且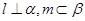 ,给出四个命题: ①若
,给出四个命题: ①若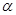 ∥
∥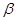 ,则
,则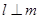 ;②若
;②若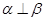 ,则
,则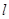 ∥m;④若
∥m;④若