题目内容
设函数f（x）=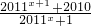
+2012sinx，x∈[-
，]的最大值为M，最小值为N，那么M+N=
- A.4011
- B.4021
- C.4031
- D.4041
B
分析：先将函数化简，确定函数为单调增函数，代入化简，即可求得结论．
解答：函数f（x）=2011-
+sinx
∵y=2011x在x∈[-，]上为增函数，∴y=在x∈[-，]上为减函数
而y=sinx在x∈[-，]上为增函数，
∴函数f（x）=2011-+sinx在x∈[-，]上为增函数，
∴M=f（），N=f（-），
∴M+N=4022-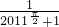
-
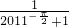=4021
故选B．
点评：本题主要考查了利用函数的单调性求函数的最大值与最小值，关键是把函数化简成可以判断单调性的形式．
分析：先将函数化简，确定函数为单调增函数，代入化简，即可求得结论．
解答：函数f（x）=2011-
+sinx∵y=2011x在x∈[-
，]上为增函数，∴y=在x∈[-，]上为减函数而y=sinx在x∈[-
，]上为增函数，∴函数f（x）=2011-
+sinx在x∈[-，]上为增函数，∴M=f（
），N=f（-），∴M+N=4022-
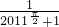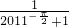-=4021故选B．
点评：本题主要考查了利用函数的单调性求函数的最大值与最小值，关键是把函数化简成可以判断单调性的形式．
练习册系列答案
相关题目