题目内容
设P是椭圆
思路分析:由于P是椭圆![]() =1在第一象限部分的弧AB上的一动点,因此四边形OAPB的形状不定,则不能用特殊四边形的面积公式来求其最值,只能考虑把四边形分解为几个三角形,利用三角形的知识来求其面积的最大值.
=1在第一象限部分的弧AB上的一动点,因此四边形OAPB的形状不定,则不能用特殊四边形的面积公式来求其最值,只能考虑把四边形分解为几个三角形,利用三角形的知识来求其面积的最大值.
解:∵点P是椭圆![]() =1在第一象限部分的弧AB上的一点,
=1在第一象限部分的弧AB上的一点,
∴设P(6cosθ,2sinθ),θ∈(0,![]() )(图略).
)(图略).
法一:直线AB方程为![]() =1,即x+3y-6=0.欲使SOAPB最大,只需P到AB的距离最大.
=1,即x+3y-6=0.欲使SOAPB最大,只需P到AB的距离最大.
∵dP-AB=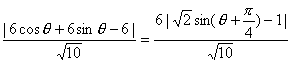 θ∈(0,
θ∈(0,![]() ),
),
∴![]() sin(θ+
sin(θ+![]() )>0.∴当θ=
)>0.∴当θ=![]() 时,dmax=
时,dmax=![]() .
.
∴(S△APB)max=![]() =6(
=6(![]() -1).
-1).
∴(SOAPB)max=![]() ·6·2+6(
·6·2+6(![]() -1)=
-1)=![]() .
.
法二:SOAPB=S△POA+S△POB=![]() ·2·6cosθ+
·2·6cosθ+![]() ·6·2sinθ
·6·2sinθ
=6(sinθ+cosθ)=![]() sin(θ+
sin(θ+![]() ),θ∈(0,
),θ∈(0,![]() ),
),
∴当θ=![]() 时,(SOAPB)max=
时,(SOAPB)max=![]() ,此时点P的坐标为(
,此时点P的坐标为(![]() ,2).
,2).
拓展延伸 分析本题所求的最值可以有几个转化方向,即转化为求S△POA+S△POB,SOAPB的最大值或者求点P到AB的最大距离,或者求SOAPB的最大值.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
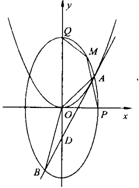 已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.