题目内容
设双曲线 的左、右焦点分别为F1(-c,0)、F2(c,0),c>0,若以F1F2为斜边的等腰直角三角形F1AF2的直角边的中点在双曲线上,则
的左、右焦点分别为F1(-c,0)、F2(c,0),c>0,若以F1F2为斜边的等腰直角三角形F1AF2的直角边的中点在双曲线上,则 等于________.
等于________.

分析:记双曲线的焦距为2C、依题意知点M在y轴上,M在y轴正半轴上,则可表示出F1和M的坐标,进而可表示出线段MF1的中点坐标代入双曲线方程,化简整理即可求得e.
解答:记双曲线的焦距为2C、依题意知点M在y轴上,
∴线段MF1的中点坐标是(-
 ,
, ).
).又∵线段MF1的中点在双曲线上,
∴
 -
- =1,即
=1,即  -
- =4,
=4, -
- =4,(e2)2-6e2+4=0,e2=3±
=4,(e2)2-6e2+4=0,e2=3± .又e2>1,
.又e2>1,∴e2=3+

∵(
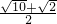 )2=3+
)2=3+ ,
,∴e=
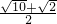 .
.故答案为
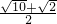 .
.点评:本题主要考查了直线与双曲线的关系以及求离心率的问题.考查了学生的综合分析问题和基本的运算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
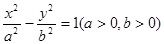 的左、右焦点分别为
的左、右焦点分别为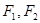 ,离心率为
,离心率为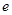 ,过
,过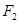 的直线与双曲线的右支交于
的直线与双曲线的右支交于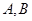 两点,若
两点,若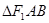 是以
是以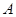 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则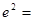 _______.
_______.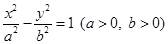 的左、右焦点分别为
的左、右焦点分别为 是双曲线渐近线上的一点,
是双曲线渐近线上的一点,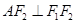 ,原点
,原点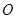 到直线
到直线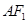 的距离为
的距离为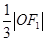 ,则渐近线的斜率为 (
)
,则渐近线的斜率为 (
)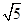 或
或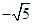 (B)
(B)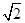 或
或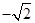 (C)1或
(C)1或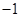 (D)
(D)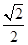 或
或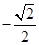
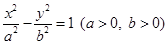 的左、右焦点分别为
的左、右焦点分别为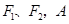 是双曲线渐近线上的一点,
是双曲线渐近线上的一点,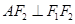 ,原点
,原点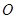 到直线
到直线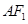 的距离为
的距离为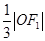 ,则渐近线的斜率为 (
)
,则渐近线的斜率为 (
)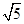 或
或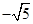 (B)
(B)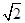 或
或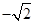 (C)1或
(C)1或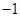 (D)
(D)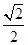 或
或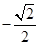
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,过点
,过点 、
、 .若△
.若△ 为正三角形,则该双曲线的离心率为
为正三角形,则该双曲线的离心率为
 B.
B. C.
C. D.
D.