题目内容
【题目】设函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)利用![]() ,化简函数求出切点坐标,求解是的导数,得到切线方程的斜率,即可求解切线方程.(2)求出函数的导数,利用导数为
,化简函数求出切点坐标,求解是的导数,得到切线方程的斜率,即可求解切线方程.(2)求出函数的导数,利用导数为![]() ,得到极值点,然后①当
,得到极值点,然后①当![]() 时,②当
时,②当![]() ,③当
,③当![]() ,④当
,④当![]() ,⑤当
,⑤当![]() ,分别求解函数的单调性推出最值,解得
,分别求解函数的单调性推出最值,解得![]() 的取值范围.第(2)问另解:
的取值范围.第(2)问另解:![]() 当
当![]() 时的最大值为
时的最大值为![]() ,等价于
,等价于![]() 对于
对于![]() 恒成立,转化
恒成立,转化![]() 的函数,构造新函数,利用增函数的导数求解最值即可.
的函数,构造新函数,利用增函数的导数求解最值即可.
试题解析:(1)当![]() 时,
时,![]()
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(2)![]()
令![]() 得
得![]()
①当![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增
递增
当![]() ,
,![]()
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增
递增
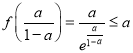 解得
解得![]() 所以
所以![]()
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递减,
递减,![]()
④当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增
递增
![]() 解得
解得![]() 所以
所以![]()
⑤当![]() 即
即![]() 时,
时,![]() 在
在![]() 递增,
递增,![]() 不合题意
不合题意
综上所述:![]() 的取值范围为
的取值范围为![]()
第(2)问另解:![]()
![]() 当
当![]() 时的最大值为
时的最大值为![]() ,等价于
,等价于![]() 对于
对于![]() 恒成立
恒成立
可化为![]() 对于
对于![]() 恒成立
恒成立
令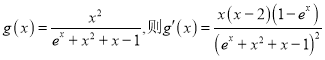
于是![]() 在
在![]() 递增,在
递增,在![]() 递减
递减
![]()
![]() 的取值范围为
的取值范围为![]()

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目