题目内容
设函数f(x)= +sinx的所有正的极小值点从小到大排成的数列为{xn}。
+sinx的所有正的极小值点从小到大排成的数列为{xn}。
(1)求数列{xn}。
(2)设{xn}的前n项和为Sn,求sinSn。
 +sinx的所有正的极小值点从小到大排成的数列为{xn}。
+sinx的所有正的极小值点从小到大排成的数列为{xn}。(1)求数列{xn}。
(2)设{xn}的前n项和为Sn,求sinSn。
解:(1)求导函数可得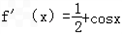 ,
,
令f′(x)=0,可得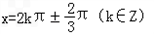
令f′(x)>0,可得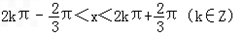 ;
;
令f′(x)<0,可得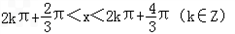
∴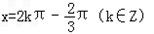 时,f(x)取得极小值
时,f(x)取得极小值
∴xn=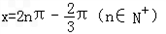
(2)Sn=x1+x2+…+xn=2π(1+2+…+n)﹣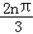 =n(n+1)π﹣
=n(n+1)π﹣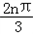
∴当n=3k(k∈N+)时,sinSn=sin(﹣2kπ)=0;
当n=3k-1(k∈N+)时,sinSn=sin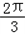 =
=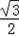 ;
;
当n=3k-2(k∈N+)时,sinSn=sin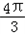 =-
=-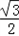 。
。
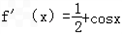 ,
,令f′(x)=0,可得
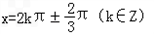
令f′(x)>0,可得
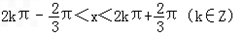 ;
;令f′(x)<0,可得
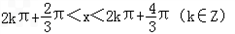
∴
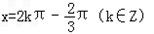 时,f(x)取得极小值
时,f(x)取得极小值∴xn=
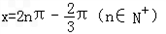
(2)Sn=x1+x2+…+xn=2π(1+2+…+n)﹣
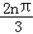 =n(n+1)π﹣
=n(n+1)π﹣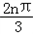
∴当n=3k(k∈N+)时,sinSn=sin(﹣2kπ)=0;
当n=3k-1(k∈N+)时,sinSn=sin
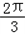 =
=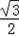 ;
;当n=3k-2(k∈N+)时,sinSn=sin
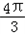 =-
=-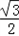 。
。
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目