题目内容
已知函数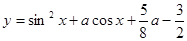 在
在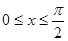 上的最大值
上的最大值
为1,求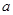 的值。
的值。
【答案】

【解析】
试题分析:


∵ ,∴
,∴ ,故有
,故有
(1)当 ,即
,即 时,则当
时,则当 时,函数取得最大值为
时,函数取得最大值为 ,
,
 =1,解得
=1,解得 (不合题意,舍去)。
(不合题意,舍去)。
(2)当 ,即
,即 时,则当
时,则当 时,,函数取得最大值为
时,,函数取得最大值为 ,
,
 =1,解得
=1,解得 (不合题意,舍去)。
(不合题意,舍去)。
(3)当 ,即
,即 时,则当
时,则当 时,函数取得最大值为
时,函数取得最大值为 ,
, =1,整理,得
=1,整理,得 ,解得
,解得 或
或 (不合题意)。
(不合题意)。
综上所述,所求 的值为
的值为 .
.
考点:三角函数的最值
点评:本题主要考查两角差的正弦公式,二次函数的最值的求法,体现了分类讨论的数学思想,注意t的取值范围,这是解题的易错点.

练习册系列答案
相关题目
 ,
, ,已知函数
,已知函数 在
在 上的最大值为6.
上的最大值为6. 的值;
的值; ,
, .求
.求 的值.
的值. 在
在 上的最大值为
上的最大值为 ,则
,则 B.1 C.
B.1 C. D.2
D.2 在
在 上的最大值是3,最小值是2,则实数
上的最大值是3,最小值是2,则实数 的取值范围是
.
的取值范围是
.
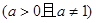 在
在 上的最大值与最小值之和为
上的最大值与最小值之和为 ,记
,记 。
。 的值;
的值; ;
; 的值
的值