题目内容
某市对该市小微企业资金短缺情况统计如下表:
(Ⅰ)试估计该市小微企业资金缺额的平均值;
(Ⅱ)某银行为更好的支持小微企业健康发展,从其第一批注资的A行业4家小微企业和B行业的3家小微企业中随机选取4家小微企业,进行跟踪调研.设选取的4家小微企业 中是B行业的小微企业的个数为随机变量ξ,求ξ的分布列.
| 小微企业短缺资金金额(万元) | [0,20] | [20,40] | [40,60] | [60,80] | [80,100] |
| 频率 | 0.05 | 0.1 | 0.35 | 0.30 | 0.20 |
(Ⅱ)某银行为更好的支持小微企业健康发展,从其第一批注资的A行业4家小微企业和B行业的3家小微企业中随机选取4家小微企业,进行跟踪调研.设选取的4家小微企业 中是B行业的小微企业的个数为随机变量ξ,求ξ的分布列.
分析:(Ⅰ)利用统计表中的数据,结合平均数计算公式能求了该市小微企业资金缺额的平均值.
(Ⅱ)由题设知ξ的所有可能取值为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列.
(Ⅱ)由题设知ξ的所有可能取值为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列.
解答:(Ⅰ)解:由统计表得:该市小微企业资金缺额的平均值
=10×0.05+30×0.1+50×0.35+70×0.3+90×0.2=60(万元).-----4分
(Ⅱ)由题设ξ的所有可能取值为0,1,2,3,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,
所以ξ的分布列为
 ------13分.
------13分.
. |
| x |
(Ⅱ)由题设ξ的所有可能取值为0,1,2,3,
P(ξ=0)=
| ||
|
| 1 |
| 35 |
P(ξ=1)=
| ||||
|
| 12 |
| 35 |
P(ξ=2)=
| ||||
|
| 18 |
| 35 |
P(ξ=3)=
| ||||
|
| 4 |
| 35 |
所以ξ的分布列为
 ------13分.
------13分.点评:本题考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,仔细解答,注意排列组合知识的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某市对该市的重点中学2006年的高考进行统计,随机抽察了244名学生,得到如下表格:
| 语文 | 数学 | 英语 | 综合科目 | |||||
| 上线 | 不上线 | 上线 | 不上线 | 上线 | 不上线 | 上线 | 不上线 | |
| 总分上线201人 | 174 | 27 | 178 | 23 | 176 | 25 | 175 | 26 |
| 总分不上线43人 | 30 | 13 | 23 | 20 | 24 | 19 | 26 | 17 |
| 总计 | 204 | 40 | 201 | 43 | 200 | 44 | 201 | 43 |
试求各科目上线与总分上线之间的关系有多大把握,并求出哪一科目与总分上线的关系最大?
某市对该市小微企业资金短缺情况统计如下表:
(Ⅰ)试估计该市小微企业资金缺额的平均值;
(Ⅱ)某银行为更好的支持小微企业健康发展,从其第一批注资的A行业4家小微企业和 B行业的3家小微企业中随机选取4家小微企业,进行跟踪调研.设选取的4家小微企业 中是B行业的小微企业的个数为随机变量ξ,求ξ的分布列.
| 小微企业短缺资金金额(万元) | [0,20] | [20,40] | [40,60] | [60,80] | [80,100] |
| 频率 | 0.05 | 0.1 | 0.35 | 0.30 | 0.20 |
(Ⅱ)某银行为更好的支持小微企业健康发展,从其第一批注资的A行业4家小微企业和 B行业的3家小微企业中随机选取4家小微企业,进行跟踪调研.设选取的4家小微企业 中是B行业的小微企业的个数为随机变量ξ,求ξ的分布列.
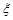 的分布列和数学期望.
的分布列和数学期望.