题目内容
已知两点![]() 、
、![]() ,点
,点![]() 为坐标平面内的动点,满足
为坐标平面内的动点,满足![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 是动点
是动点![]() 的轨迹上的一点,
的轨迹上的一点,![]() 是
是![]() 轴上的一动点,试讨论直线
轴上的一动点,试讨论直线![]() 与圆
与圆![]() 的位置关系.
的位置关系.
同下
解析:
(1)解:设![]() ,则
,则![]() ,
,![]() ,
,![]() .2分
.2分
由![]() ,
,
得![]() ,……………………………………………4分
,……………………………………………4分
化简得![]() .
.
所以动点![]() 的轨迹方程为
的轨迹方程为![]() .………………………………5分
.………………………………5分
(2)解:由![]() 在轨迹
在轨迹![]() 上,则
上,则![]() ,解得
,解得![]() ,即
,即![]() .……6分
.……6分
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,此时直线
,此时直线![]() 与圆
与圆![]() 相离.……………7分
相离.……………7分
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,即
,即![]() .………………8分
.………………8分
圆![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离
的距离 ,
,
令 ,解得
,解得![]() ;
;
令 ,解得
,解得![]() ;
;
令 ,解得
,解得![]() .
.
综上所述,当![]() 时,直线
时,直线![]() 与圆
与圆![]() 相交;
相交;
当![]() 时,直线
时,直线![]() 与圆
与圆![]() 相切;
相切;
当![]() 时,直线
时,直线![]() 与圆
与圆![]() 相离.………………14分
相离.………………14分

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
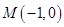 、
、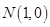 ,点
,点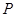 为坐标平面内的动点,满足
为坐标平面内的动点,满足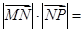
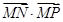 .
.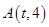 是动点
是动点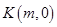 是
是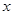 轴上的一动点,试讨论直线
轴上的一动点,试讨论直线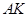 与圆
与圆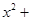
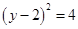 的位置关系.
的位置关系.