题目内容
设各项都不同的等比数列{an}的首项为a,公比为q,前n项和为Sn,要使数列{p-Sn}为等比数列,则必有q=________.
1-
分析:根据等比数列的前n项和公式求出Sn,进而求出数列{p-Sn}的通项公式,再根据等比数列的通项公式判断若数列{p-Sn}为等比数列,满足的条件即可.
解答:∵数列{an}为各项都不同的等比数列,∴Sn=
∴p-Sn=p- =
=
若数列{p-Sn}为等比数列,则 =0,
=0,
即p-pq-a=0,∴q=1-
故答案为:1-
点评:本题主要考察了等比数列的通项公式与前n项和公式的应用,属于数列的常规题.

分析:根据等比数列的前n项和公式求出Sn,进而求出数列{p-Sn}的通项公式,再根据等比数列的通项公式判断若数列{p-Sn}为等比数列,满足的条件即可.
解答:∵数列{an}为各项都不同的等比数列,∴Sn=

∴p-Sn=p-
 =
=
若数列{p-Sn}为等比数列,则
 =0,
=0,即p-pq-a=0,∴q=1-

故答案为:1-

点评:本题主要考察了等比数列的通项公式与前n项和公式的应用,属于数列的常规题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
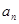 }的首项为
}的首项为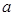 ,公比为
,公比为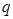 ,前
,前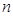 项和为
项和为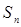 ,要使数列{
,要使数列{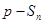 }为等比数列,则必有
}为等比数列,则必有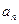 }的首项为
}的首项为 ,公比为
,公比为 ,前
,前 项和为
项和为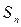 ,要使数列{
,要使数列{ }为等比数列,则必有
}为等比数列,则必有 }的首项为
}的首项为 ,公比为
,公比为 ,前
,前 项和为
项和为 ,要使数列{
,要使数列{ }为等比数列,则必有
}为等比数列,则必有