题目内容
设各项都不同的等比数列{an}的首项为a,公比为q,前n项和为Sn,要使数列{p-Sn}为等比数列,则必有q=______.
∵数列{an}为各项都不同的等比数列,∴Sn=
∴p-Sn=p-
=
-
若数列{p-Sn}为等比数列,则
=0,
即p-pq-a=0,∴q=1-
故答案为:1-
| a(1-qn) |
| 1-q |
∴p-Sn=p-
| a(1-qn) |
| 1-q |
| p-pq-a |
| 1-q |
| a qn |
| 1-q |
若数列{p-Sn}为等比数列,则
| p-pq-a |
| 1-q |
即p-pq-a=0,∴q=1-
| a |
| p |
故答案为:1-
| a |
| p |

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
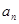 }的首项为
}的首项为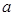 ,公比为
,公比为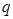 ,前
,前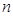 项和为
项和为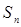 ,要使数列{
,要使数列{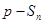 }为等比数列,则必有
}为等比数列,则必有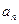 }的首项为
}的首项为 ,公比为
,公比为 ,前
,前 项和为
项和为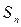 ,要使数列{
,要使数列{ }为等比数列,则必有
}为等比数列,则必有 }的首项为
}的首项为 ,公比为
,公比为 ,前
,前 项和为
项和为 ,要使数列{
,要使数列{ }为等比数列,则必有
}为等比数列,则必有