题目内容
9、设R上的函数f（x）满足f（4）=1，它的导函数的图象如图，若正数a、b满足f（2a+b）＜1，则z=a+b的取值范围是（ ）分析：根据图象可知，函数f（x）在（0，+∞）单调递增，在（-∞，0）单调递减，从而由f（2a+b）＜1及f（4）=1，a＞0，b＞0可得，0＜2a+b＜4，利用线性规划做出0＜2a+b＜4，所表示的平面区域，求z=a+b的取值范围
解答：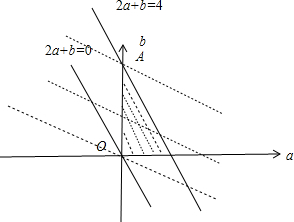
解：根据图象可知，函数f（x）在（0，+∞）单调递增，在（-∞，0）单调递减
f（2a+b）＜1，f（4）=1，a＞0，b＞0
f（2a+b）＜f（4），则0＜2a+b＜4，
利用线性规划的知识可得0＜2a+b＜4，所表示的平面区域如图所示的阴影部分
当直线z=a+b过原点时z=0，当直线z=a+b过A（0，4）时z=4
所以，0＜z＜4
故选：B
解：根据图象可知，函数f（x）在（0，+∞）单调递增，在（-∞，0）单调递减f（2a+b）＜1，f（4）=1，a＞0，b＞0
f（2a+b）＜f（4），则0＜2a+b＜4，
利用线性规划的知识可得0＜2a+b＜4，所表示的平面区域如图所示的阴影部分
当直线z=a+b过原点时z=0，当直线z=a+b过A（0，4）时z=4
所以，0＜z＜4
故选：B
点评：本题综合考查了导数与函数的单调性的关系，二元一次不等式表示平面区域，线性规划求解最优解等问题的综合，是一道很好的试题
练习册系列答案
相关题目
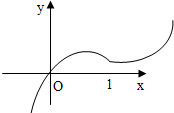设R上的函数f（x）满足f（4）=1，它的导函数的图象如图，若正数a、b满足f（2a+b）＜1，则z=a+b的取值范围是