题目内容
已知椭圆与双曲线x2-y2=0有相同的焦点,且离心率为 .
.
(1)求椭圆的标准方程;
(2)过点P(0,1)的直线与该椭圆交于A,B两点,O为坐标原点,若 =2
=2 ,求△AOB的面积.
,求△AOB的面积.
 .
.(1)求椭圆的标准方程;
(2)过点P(0,1)的直线与该椭圆交于A,B两点,O为坐标原点,若
 =2
=2 ,求△AOB的面积.
,求△AOB的面积.(1) =1(2)
=1(2)
 =1(2)
=1(2)
(1)设椭圆方程为 =1,a>b>0,
=1,a>b>0,
由c= ,
, =
= ,可得a=2,b2=a2-c2=2,
,可得a=2,b2=a2-c2=2,
所以椭圆的标准方程为 =1.
=1.
(2)设A(x1,y1),B(x2,y2),由 =2
=2 ,得
,得 可得x1=-2x2.①
可得x1=-2x2.①
设过点P的直线方程为y=kx+1,代入椭圆方程,整理得(2k2+1)x2+4kx-2=0,
则x1+x2=- ,②x1x2=
,②x1x2= ,③
,③
由①②得x2= ,将x1=-2x2代入③得
,将x1=-2x2代入③得 =
= ,
,
所以 =
= ,解得k2=
,解得k2= .
.
又△AOB的面积S= |OP|·|x1-x2|=
|OP|·|x1-x2|= ·
· =
= .所以△AOB的面积是
.所以△AOB的面积是 .
.
 =1,a>b>0,
=1,a>b>0,由c=
 ,
, =
= ,可得a=2,b2=a2-c2=2,
,可得a=2,b2=a2-c2=2,所以椭圆的标准方程为
 =1.
=1.(2)设A(x1,y1),B(x2,y2),由
 =2
=2 ,得
,得 可得x1=-2x2.①
可得x1=-2x2.①设过点P的直线方程为y=kx+1,代入椭圆方程,整理得(2k2+1)x2+4kx-2=0,
则x1+x2=-
 ,②x1x2=
,②x1x2= ,③
,③由①②得x2=
 ,将x1=-2x2代入③得
,将x1=-2x2代入③得 =
= ,
,所以
 =
= ,解得k2=
,解得k2= .
.又△AOB的面积S=
 |OP|·|x1-x2|=
|OP|·|x1-x2|= ·
· =
= .所以△AOB的面积是
.所以△AOB的面积是 .
.
练习册系列答案
相关题目
 +
+ =1(a>b>0)的右焦点为F(1,0),且点(-1,
=1(a>b>0)的右焦点为F(1,0),且点(-1,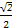 )在椭圆C上.
)在椭圆C上. ,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明:
,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明: ·
· 为定值.
为定值. :方程
:方程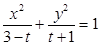 所表示的曲线为焦点在
所表示的曲线为焦点在 轴上的椭圆;命题
轴上的椭圆;命题 :实数
:实数 满足不等式
满足不等式 .
. 的取值范围.
的取值范围.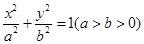 的一个焦点
的一个焦点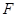 与抛物线
与抛物线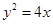 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为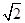 ,倾斜角为
,倾斜角为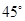 的直线
的直线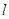 过点
过点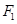 ,问抛物线
,问抛物线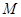 ,使得
,使得 +
+ =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF= ,则C的离心率为( )
,则C的离心率为( )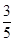


 +y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.
+y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.

 的两焦点,过点F2的直线交椭圆于A,B两点.在
的两焦点,过点F2的直线交椭圆于A,B两点.在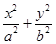 =1(a>b>0)的左、右顶点分别是A、B,左、右焦点分别是F1、F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为________.
=1(a>b>0)的左、右顶点分别是A、B,左、右焦点分别是F1、F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为________.