题目内容
抛物线y=4x2的准线方程是（ ）A．x=1
B．x=-
C．y=-1
D．y=-
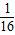
【答案】分析：先将抛物线方程化为标准方程，进而可求抛物线的准线方程．
解答：解：由题意，抛物线的标准方程为x2=
y，
∴p=
，开口朝上，
∴准线方程为y=-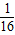
；
故选D．
点评：本题的考点是抛物线的简单性质，主要考查抛物线的标准方程，属于基础题．
解答：解：由题意，抛物线的标准方程为x2=
y，∴p=
，开口朝上，∴准线方程为y=-
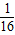；故选D．
点评：本题的考点是抛物线的简单性质，主要考查抛物线的标准方程，属于基础题．
练习册系列答案
相关题目
抛物线y=-4x2的准线方程是（ ）
A、x=
| ||
| B、x=1 | ||
| C、y=1 | ||
D、y=
|
已知命题p：函数f(x)=
e-
在区间（0，+∞）上单调递减；q：双曲线
-
=1的左焦点到抛物线y=4x2的准线的距离为2．则下列命题正确的是（ ）
| 1 | ||
|
| x2 |
| 2 |
| x2 |
| 4 |
| y2 |
| 5 |
| A、p∨q |
| B、p∧q |
| C、（?p）∧q |
| D、q |