题目内容
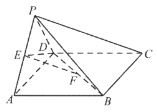
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,
中点,![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() ;(Ⅲ)不存在;说明见解析
;(Ⅲ)不存在;说明见解析
【解析】
(Ⅰ)利用三角形中位线证得![]() ,利用线面平行判定定理证得结果;(Ⅱ)取
,利用线面平行判定定理证得结果;(Ⅱ)取![]() 中点
中点![]() ,利用面面垂直的性质和正方形的特点可证明出
,利用面面垂直的性质和正方形的特点可证明出![]() 两两互相垂直,从而可以
两两互相垂直,从而可以![]() 为原点建立空间直角坐标系;由线面垂直关系可得面
为原点建立空间直角坐标系;由线面垂直关系可得面![]() 法向量为
法向量为![]() ;再利用向量法求解出平面
;再利用向量法求解出平面![]() 法向量,利用向量夹角公式求得余弦值,再求得正弦值;(Ⅲ)令
法向量,利用向量夹角公式求得余弦值,再求得正弦值;(Ⅲ)令![]() ,可表示出
,可表示出![]() ,若
,若![]() 平面
平面![]() ,则
,则![]() 与平面
与平面![]() 法向量共线,由共线定理得到方程,方程无解,可知不存在
法向量共线,由共线定理得到方程,方程无解,可知不存在![]() .
.
(Ⅰ)连接![]()
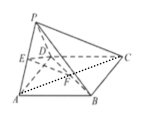
![]() 四边形
四边形![]() 为正方形
为正方形 ![]() 为
为![]() 中点
中点
又![]() 为
为![]() 中点
中点 ![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]()
![]()
![]()
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() 四边形
四边形![]() 为正方形且
为正方形且![]()
![]()
![]() 以
以![]() 为原点,
为原点,![]() 所在直线为坐标轴建立如下图所示的空间直角坐标系
所在直线为坐标轴建立如下图所示的空间直角坐标系
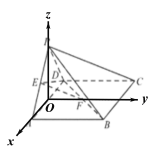
则![]() ,
,![]() ,
,![]() ,
,![]()
![]() 平面
平面![]() 即为平面
即为平面![]() ,
,![]() 平面
平面![]()
![]() 即为平面
即为平面![]() 的一个法向量,即
的一个法向量,即![]()
设平面![]() 的法向量
的法向量![]()
又![]() ,
,![]()
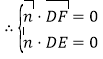 ,即
,即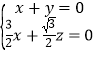 ,令
,令![]() ,则
,则![]() ,
,![]()
![]()
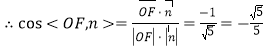
![]()
即二面角![]() 的正弦值为:
的正弦值为:![]()
(Ⅲ)令![]()
![]() ,
,![]()
![]()
若![]() 平面
平面![]() ,则
,则![]() ,又
,又![]()
![]() ,方程无解
,方程无解
![]() 棱
棱![]() 上不存在一点
上不存在一点![]() ,使
,使![]() 平面
平面![]()

【题目】某汽车公司为调查4S店个数对该公司汽车销量的影响,对同等规模的A,B,C,D四座城市的4S店一个月某型号汽车销量进行了统计,结果如下表:
城市 | A | B | C | D |
4S店个数x | 3 | 4 | 6 | 7 |
销售台数y | 18 | 26 | 34 | 42 |
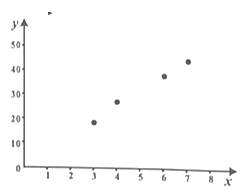
(1)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(2)根据统计每个城市汽车的盈利![]() (万元)与该城市4S店的个数x符合函数
(万元)与该城市4S店的个数x符合函数![]() ,
,![]() ,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
附:回归方程![]() 中的斜率和截距的最小二乘法估计公式分别为:
中的斜率和截距的最小二乘法估计公式分别为: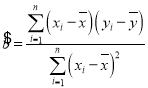 ,
,![]()
【题目】对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?